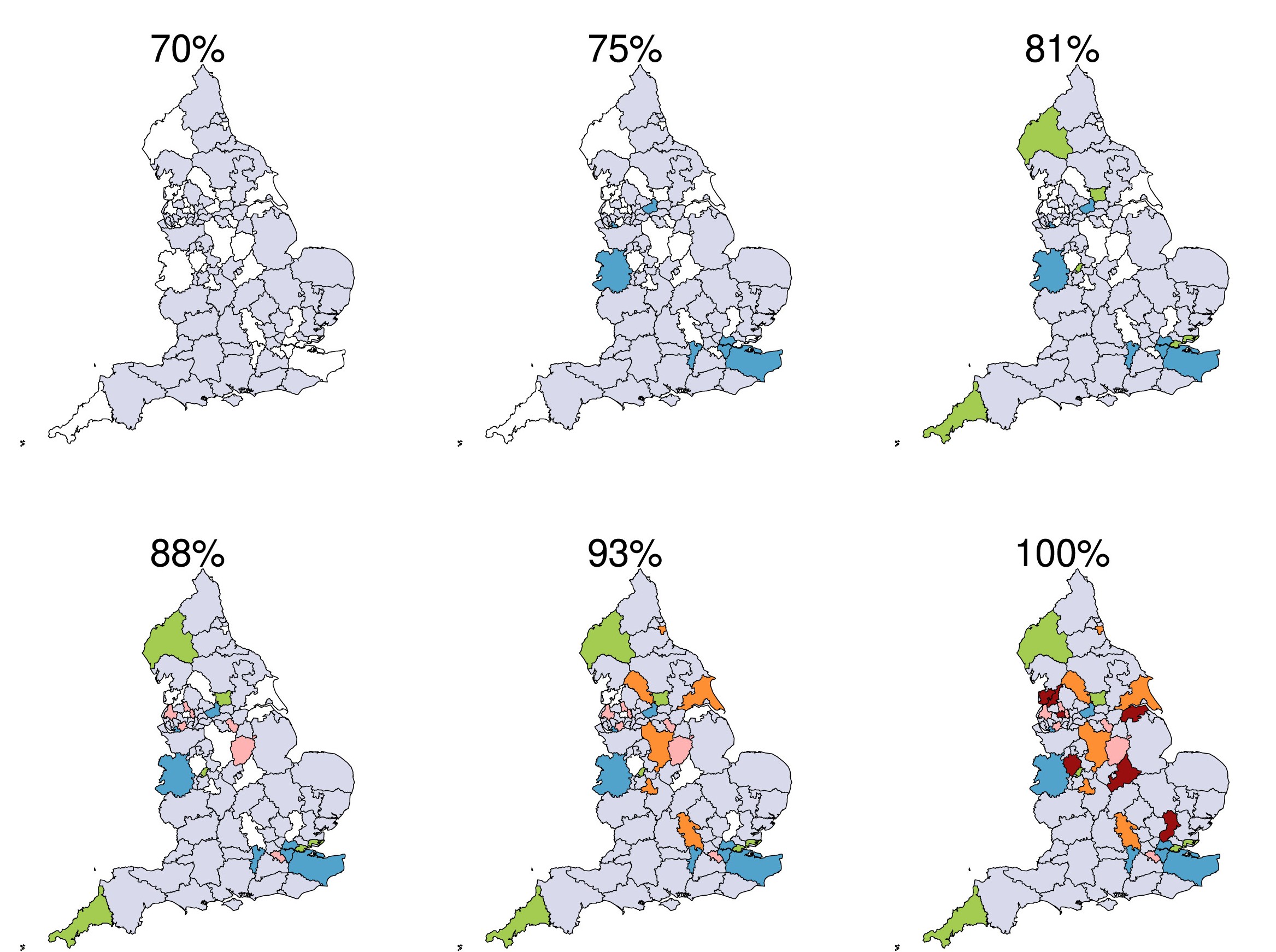
Multivariate Spatio-temporal Modelling for Completing Cancer Registries and Forecasting Incidence
Cancer data, particularly cancer incidence and mortality, are fundamental to understand the cancer burden, to set targets for cancer control and to evaluate the evolution of the implementation of a cancer control policy. However, the complexity of data collection, classification, validation and processing result in cancer incidence figures often lagging two to three years behind the calendar year. In response, national or regional population-based cancer registries (PBCRs) are increasingly interested in methods for forecasting cancer incidence. However, in many countries there is an additional difficulty in projecting cancer incidence as regional registries are usually not established in the same year and therefore cancer incidence data series between different regions of a country are not harmonised over time. This study addresses the challenge of forecasting cancer incidence with incomplete data at both regional and national levels. To achieve this, we propose the use of multivariate spatio-temporal shared component models that jointly model mortality data and available cancer incidence data. We evaluate the performance of these multivariate models using lung cancer incidence data and the corresponding number of deaths reported in England for the period 2001-2019. Model performance was assessed using different predictive measures to select the best model.
View Full-Text R code available at GitHub repository
A Proposal for Homoskedastic Modeling With Conditional Auto-Regressive Distributions
Conditional auto-regressive (CAR) distributions are widely used to deal with spatial dependence in the geographic analysis of areal data. These distributions establish multivariate dependence networks by defining conditional relationships between neighboring units, resulting in positive dependence among nearby observations. Despite their practical convenience and well-founded principles, the conditional nature of CAR distributions can lead to undesirable marginal properties, such as inherent heteroskedasticity assumptions that may significantly impact the posterior distributions. In this paper, we highlight the variance issues associated with CAR distributions, particularly focusing on edge effects and issues related to the region's geometry. We show that edge effects may be more pronounced and widespread in disease mapping studies than previously anticipated. To address these heteroskedasticity concerns, we introduce a new conditional autoregressive distribution designed to mitigate these problems. We demonstrate how this distribution effectively diminishes the practical issues identified in earlier models.
View Full-Text R code available at GitHub repository
On prior smoothing with discrete spatial data in the context of disease mapping
Disease mapping attempts to explain observed health event counts across areal units, typically using Markov random field models. These models rely on spatial priors to account for variation in raw relative risk or rate estimates. Spatial priors introduce some degree of smoothing, wherein, for any particular unit, empirical risk or incidence estimates are either adjusted towards a suitable mean or incorporate neighbor-based smoothing. While model explanation may be the primary focus, the literature lacks a comparison of the amount of smoothing introduced by different spatial priors. Additionally, there has been no investigation into how varying the parameters of these priors influences the resulting smoothing. This study examines seven commonly used spatial priors through both simulations and real data analyses. Using areal maps of peninsular Spain and England, we analyze smoothing effects using two datasets with associated populations at risk. We propose empirical metrics to quantify the smoothing achieved by each model and theoretical metrics to calibrate the expected extent of smoothing as a function of model parameters. We employ areal maps in order to quantitatively characterize the extent of smoothing within and across the models as well as to link the theoretical metrics to the empirical metrics.
View Full-Text R code available at GitHub repository
A fast approach for analyzing spatio-temporal patterns in ischemic heart disease mortality across US counties (1999–2021)
Ischaemic heart disease (IHD) remains the primary cause of mortality in the US. This study focuses on using spatio-temporal disease mapping models to explore the temporal trends of IHD at the county level from 1999 to 2021. To manage the computational burden arising from the high-dimensional data, we employ scalable Bayesian models using a ”divide and conquer” strategy. This approach allows for fast model fitting and serves as an efficient procedure for screening spatio-temporal patterns. Additionally, we analyze trends in four regional subdivisions, West, Midwest, South and Northeast, and in urban and rural areas. The dataset on IHD contains missing data, and we propose a procedure to impute the omitted information. The results show a slowdown in the decrease of IHD mortality in the US after 2014 with a slight increase noted after 2019. However, differences exists among the counties, the four big geographical regions, and rural and urban areas.
View Full-Text R code available at GitHub repository

Automatic cross-validation in structured models: Is it time to leave out leave-one-out?
Standard techniques such as leave-one-out cross-validation (LOOCV) might not be suitable for evaluating the predictive performance of models incorporating structured random effects. In such cases, the correlation between the training and test sets could have a notable impact on the model's prediction error. To overcome this issue, an automatic group construction procedure for leave-group-out cross validation (LGOCV) has recently emerged as a valuable tool for enhancing predictive performance measurement in structured models. The purpose of this paper is (i) to compare LOOCV and LGOCV within structured models, emphasizing model selection and predictive performance, and (ii) to provide real data applications in spatial statistics using complex structured models fitted with INLA, showcasing the utility of the automatic LGOCV method. First, we briefly review the key aspects of the recently proposed LGOCV method for automatic group construction in latent Gaussian models. We also demonstrate the effectiveness of this method for selecting the model with the highest predictive performance by simulating extrapolation tasks in both temporal and spatial data analyses. Finally, we provide insights into the effectiveness of the LGOCV method in modelling complex structured data, encompassing spatio-temporal multivariate count data, spatial compositional data, and spatio-temporal geospatial data.
View Full-Text R code available at GitHub repository
Multivariate Bayesian models with flexible shared interactions for analyzing spatio-temporal patterns of rare cancers
Rare cancers affect millions of people worldwide each year. However, estimating incidence or mortality rates associated with rare cancers presents important difficulties and poses new statistical methodological challenges. In this paper, we expand the collection of multivariate spatio-temporal models by introducing adaptable shared spatio-temporal components to enable a comprehensive analysis of both incidence and cancer mortality in rare cancer cases. These models allow the modulation of spatio-temporal effects between incidence and mortality, allowing for changes in their relationship over time. The new models have been implemented in INLA using r-generic constructions. We conduct a simulation study to evaluate the performance of the new spatio-temporal models. Our results show that multivariate spatio-temporal models incorporating a flexible shared spatio-temporal term outperform conventional multivariate spatio-temporal models that include specific spatio-temporal effects for each health outcome. We use these models to analyze incidence and mortality data for pancreatic cancer and leukaemia among males across 142 administrative health care districts of Great Britain over a span of nine biennial periods (2002–2019).
View Full-Text R code available at GitHub repository
A simplified spatial+ approach to mitigate spatial confounding in multivariate spatial areal models
Spatial areal models encounter the well-known and challenging problem of spatial confounding. This issue makes it arduous to distinguish between the impacts of observed covariates and spatial random effects. Despite previous research and various proposed methods to tackle this problem, finding a definitive solution remains elusive. In this paper, we propose a simplified version of the spatial+ approach that involves dividing the covariate into two components. One component captures large-scale spatial dependence, while the other accounts for short-scale dependence. This approach eliminates the need to separately fit spatial models for the covariates. We apply this method to analyse two forms of crimes against women, namely rapes and dowry deaths, in Uttar Pradesh, India, exploring their relationship with socio-demographic covariates. To evaluate the performance of the new approach, we conduct extensive simulation studies under different spatial confounding scenarios. The results demonstrate that the proposed method provides reliable estimates of fixed effects and posterior correlations between different responses.
View Full-Text R code available at GitHub repository
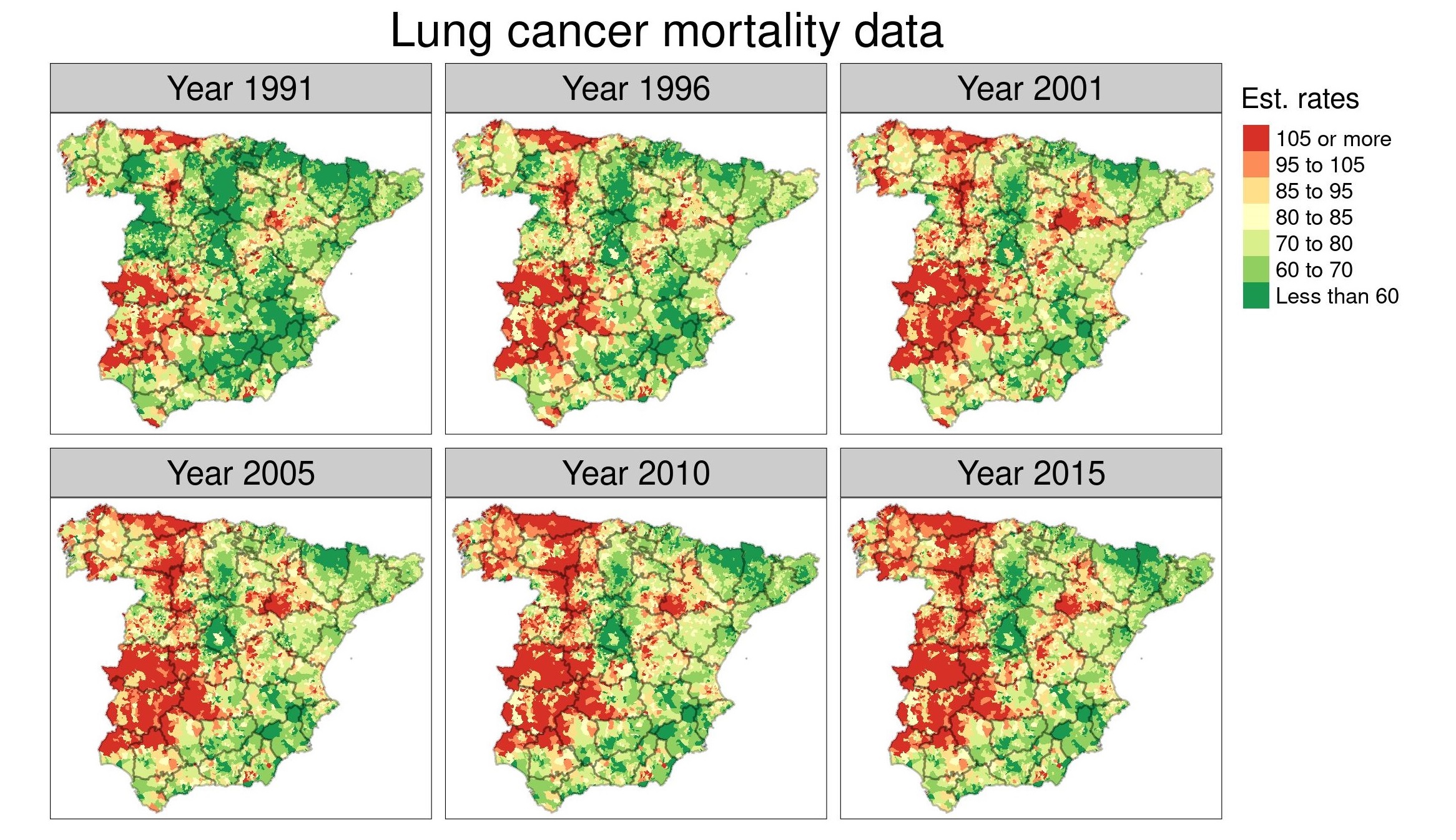
A scalable approach for short-term disease forecasting in high spatial resolution areal data
Short-term disease forecasting at specific discrete spatial resolutions has become a high-impact decision-support tool in health planning. However, when the number of areas is very large obtaining predictions can be computationally intensive or even unfeasible using standard spatiotemporal models. The purpose of this paper is to provide a method for short-term predictions in high-dimensional areal data based on a newly proposed "divide-and-conquer" approach. We assess the predictive performance of this method and other classical spatiotemporal models in a validation study that uses cancer mortality data for the 7907 municipalities of continental Spain. The new proposal outperforms traditional models in terms of mean absolute error, root mean square error, and interval score when forecasting cancer mortality 1, 2, and 3 years ahead. Models are implemented in a fully Bayesian framework using the well-known integrated nested Laplace estimation technique.
View Full-Text R code available at GitHub repository
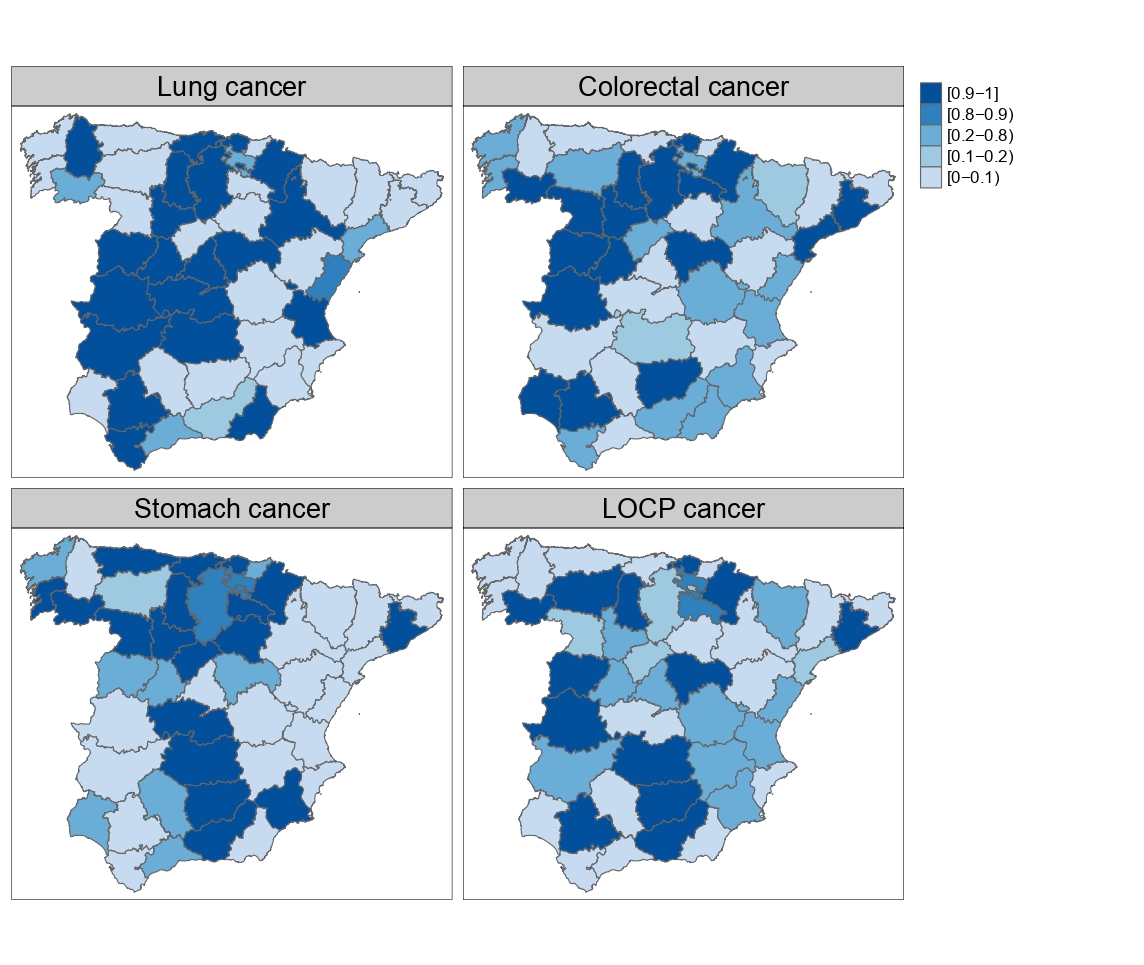
Multivariate disease mapping models to uncover hidden relationships between different cancer sites
Multivariate spatio-temporal disease mapping models offer some advantages over the univariate counterparts as they enhance borrowing of strength across diseases and unveil connections between them. Though theoretically well founded, multivariate disease mapping modelling is not generally used in practice due to computational burden and the difficulty of implementation in common statistical softwares by users without computing training. Here we consider a multivariate modelling approach to disease mapping based on M-models and we use the Bartlett decomposition of Wishart matrices to avoid over-parameterization of certain covariance matrices. The models are implemented in R through the R-INLA package so that they can be routinely used. We illustrate the methodology with a joint analysis of male mortality data for lung, colorectal, stomach and LOCP (lip, oral cavity and pharynx) cancer in continental Spain for the period 2006-2020.
View Full-Text R code available at GitHub repository
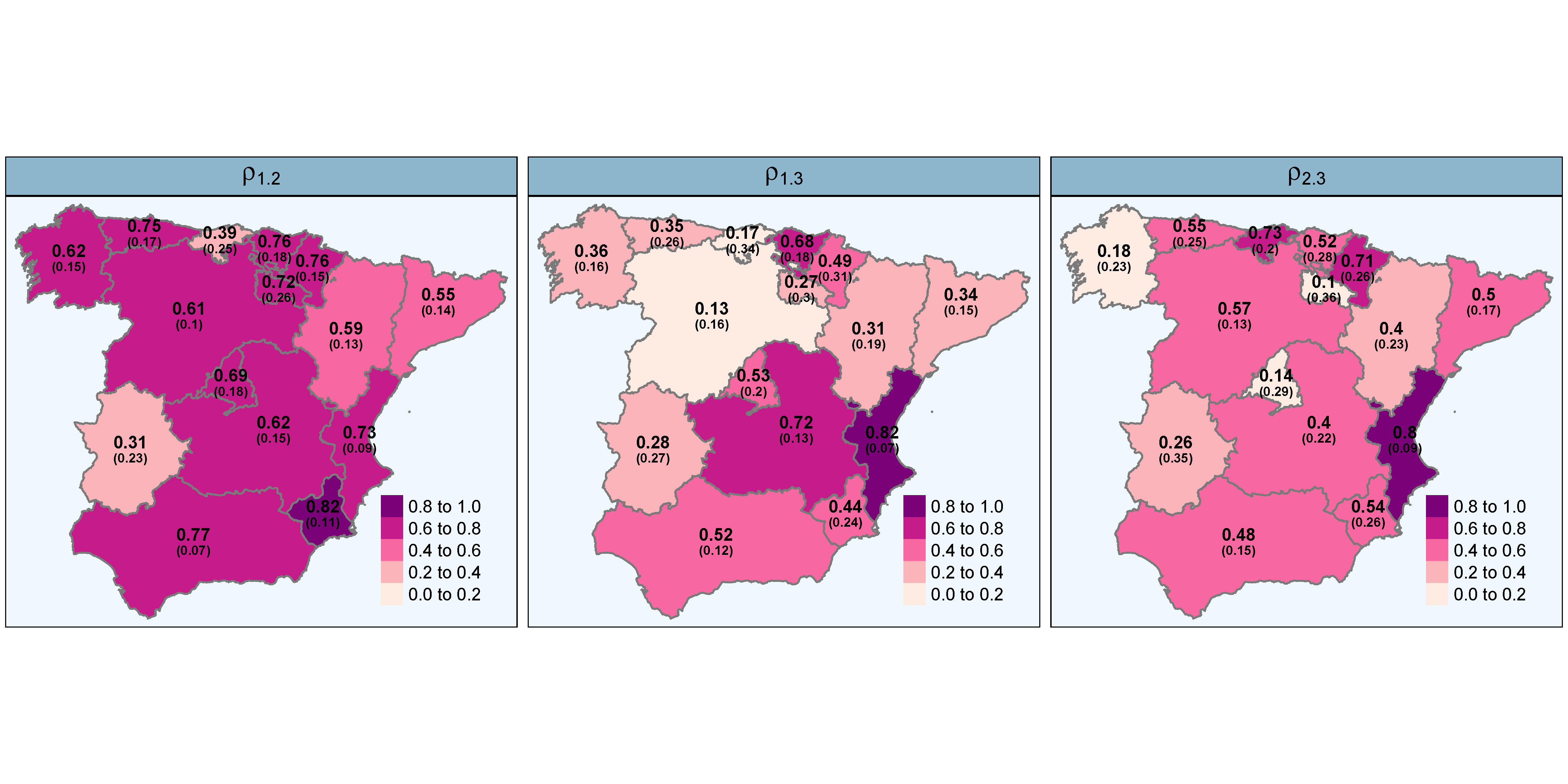
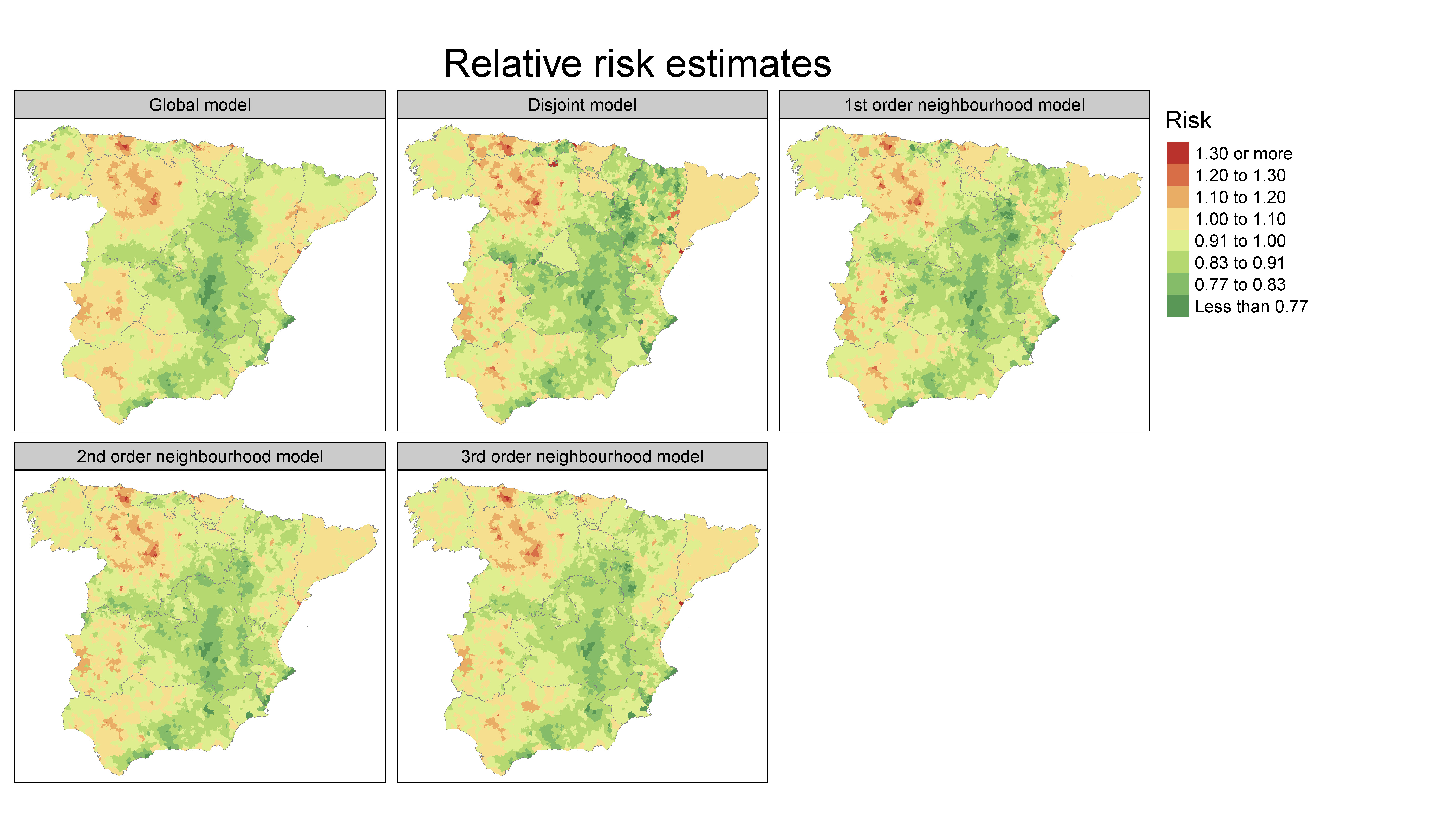
High-dimensional order-free multivariate spatial disease mapping
Despite the amount of research on disease mapping in recent years, the use of multivariate models for areal spatial data remains limited due to difficulties in implementation and computational burden. These problems are exacerbated when the number of areas is very large. In this paper, we introduce an order-free multivariate scalable Bayesian modelling approach to smooth mortality (or incidence) risks of several diseases simultaneously. The proposal partitions the spatial domain into smaller subregions, fits multivariate models in each subdivision and obtains the posterior distribution of the relative risks across the entire spatial domain. The approach also provides posterior correlations among the spatial patterns of the diseases in each partition that are combined through a consensus Monte Carlo algorithm to obtain correlations for the whole study region. We implement the proposal using integrated nested Laplace approximations (INLA) in the R package bigDM and use it to jointly analyse colorectal, lung, and stomach cancer mortality data in Spanish municipalities. The new proposal allows for the analysis of large datasets and yields superior results compared to fitting a single multivariate model. Additionally, it facilitates statistical inference through local homogeneous models, which may be more appropriate than a global homogeneous model when dealing with a large number of areas.
View Full-Text R package bigDM available at GitHub repository
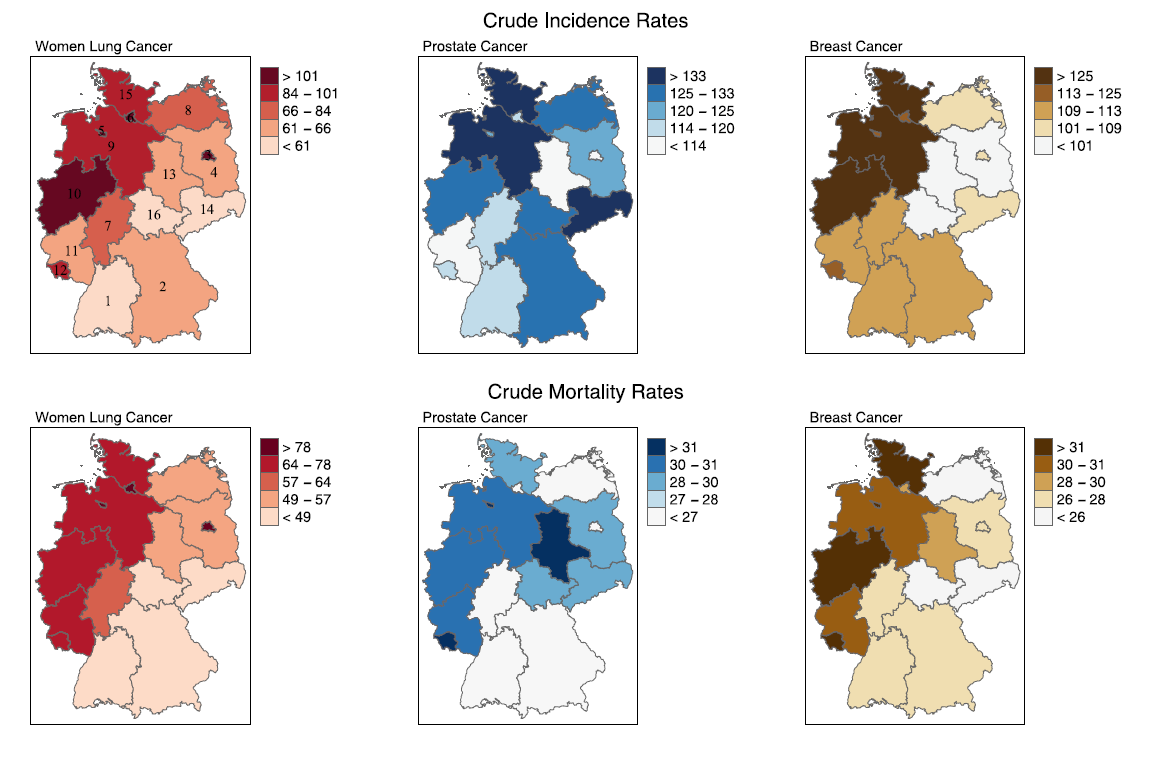
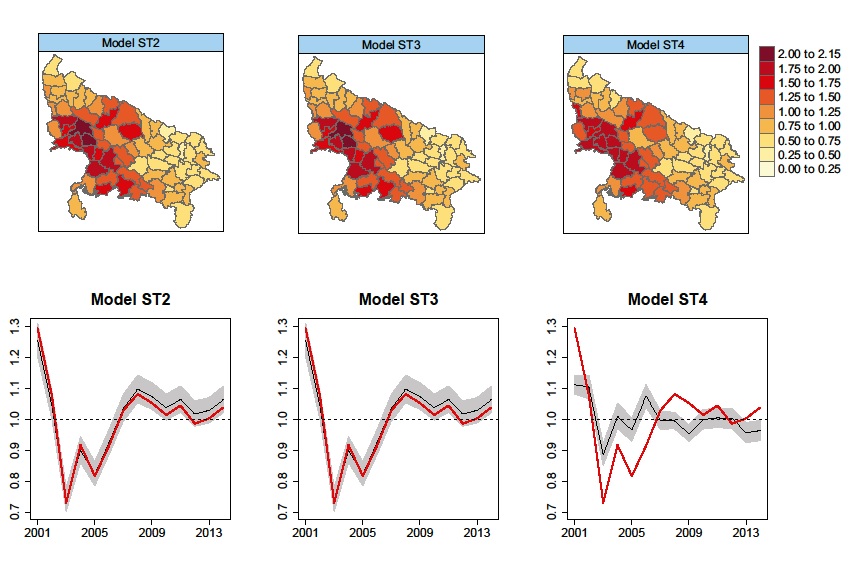
Predicting cancer incidence in regions without population-based cancer registries using mortality
Cancer incidence numbers are routinely recorded by national or regional population-based cancer registries (PBCRs). However, in most southern European countries, the local PBCRs cover only a fraction of the country. Therefore, national cancer incidence can be only obtained through estimation methods. In this paper, we predict incidence rates in areas without cancer registry using multivariate spatial models modelling jointly cancer incidence and mortality. To evaluate the proposal, we use cancer incidence and mortality data from all the German states. We also conduct a simulation study by mimicking the real case of Spain considering different scenarios depending on the similarity of spatial patterns between incidence and mortality, the levels of lethality, and varying the amount of incidence data available. The new proposal provides good interval estimates in regions without PBCRs and reduces the relative error in estimating national incidence compared to one of the most widely used methodologies.
View Full-Text R code available at GitHub repository
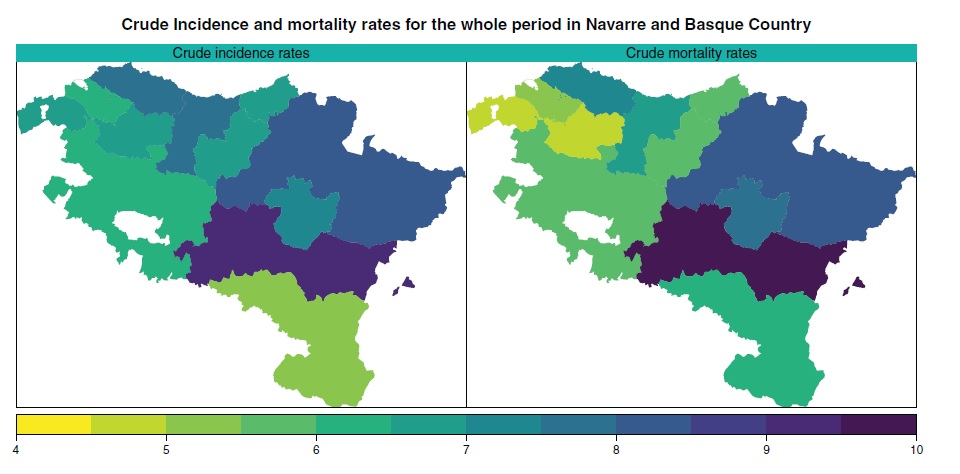
Using mortality to predict incidence for rare and lethal cancers in very small areas
Incidence and mortality figures are needed to get a comprehensive overview of cancer burden. In many countries, cancer mortality figures are routinely recorded by statistical offices, whereas incidence depends on regional cancer registries. However, due to the complexity of updating cancer registries, incidence numbers become available 3 or 4 years later than mortality figures. It is, therefore, necessary to develop reliable procedures to predict cancer incidence at least until the period when mortality data are available. Most of the methods proposed in the literature are designed to predict total cancer (except nonmelanoma skin cancer) or major cancer sites. However, less frequent lethal cancers, such as brain cancer, are generally excluded from predictions because the scarce number of cases makes it difficult to use univariate models. Our proposal comes to fill this gap and consists of modeling jointly incidence and mortality data using spatio-temporal models with spatial and age shared components. This approach allows for predicting lethal cancers improving the performance of individual models when data are scarce by taking advantage of the high correlation between incidence and mortality. A fully Bayesian approach based on integrated nested Laplace approximations is considered for model fitting and inference. A validation process is also conducted to assess the performance of alternative models. We use the new proposals to predict brain cancer incidence rates by gender and age groups in the health units of Navarre and Basque Country (Spain) during the period 2005–2008.
View Full-Text R code available at GitHub repository
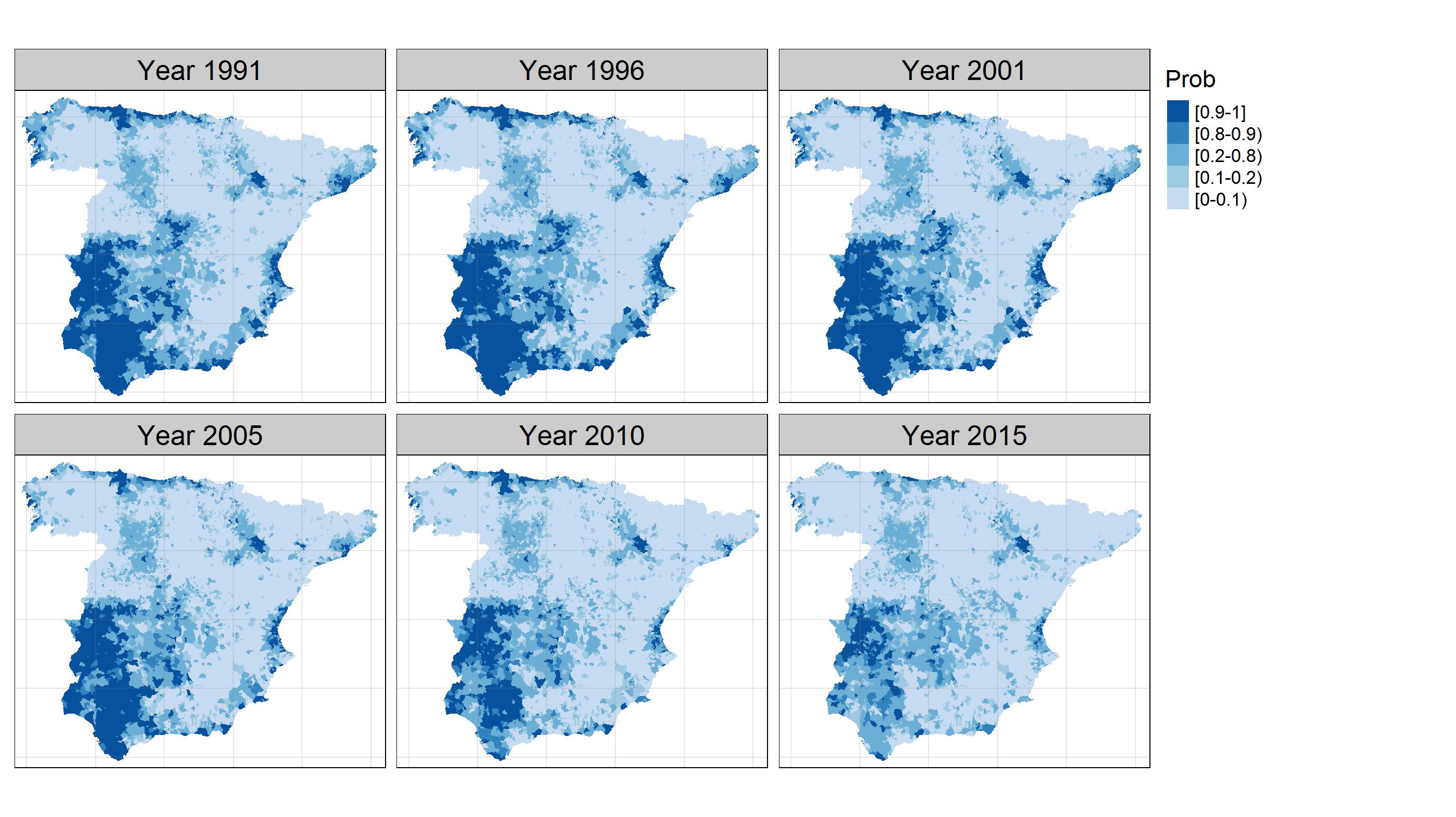
Big problems in spatio-temporal disease mapping: Methods and software
Fitting spatio-temporal models for areal data is crucial in many fields such as cancer epidemiology. However, when data sets are very large, many issues arise. The main objective of this paper is to propose a general procedure to analyze high-dimensional spatio-temporal areal data, with special emphasis on mortality/incidence relative risk estimation. We present a pragmatic and simple idea that permits hierarchical spatio-temporal models to be fitted when the number of small areas is very large. Model fitting is carried out using integrated nested Laplace approximations over a partition of the spatial domain. We also use parallel and distributed strategies to speed up computations in a setting where Bayesian model fitting is generally prohibitively time-consuming or even unfeasible. Using simulated and real data, we show that our method outperforms classical global models. We implement the methods and algorithms that we develop in the open-source R package bigDM where specific vignettes have been included to facilitate the use of the methodology for non-expert users. Our scalable methodology proposal provides reliable risk estimates when fitting Bayesian hierarchical spatio-temporal models for high-dimensional data.
View Full-Text R package bigDM available at GitHub repository
Evaluating recent methods to overcome spatial confounding
The concept of spatial confounding is closely connected to spatial regression, although no general definition has been established. A generally accepted idea of spatial confounding in spatial regression models is the change in fixed effects estimates that may occur when spatially correlated random effects collinear with the covariate are included in the model. Different methods have been proposed to alleviate spatial confounding in spatial linear regression models, but it is not clear if they provide correct fixed effects estimates. In this article, we consider some of those proposals to alleviate spatial confounding such as restricted regression, the spatial+ model, and transformed Gaussian Markov random fields. The objective is to determine which one provides the best estimates of the fixed effects. Dowry death data in Uttar Pradesh in 2001, stomach cancer incidence data in Slovenia in the period 1995-2001 and lip cancer incidence data in Scotland between the years 1975-1980 are analyzed. Several simulation studies are conducted to evaluate the performance of the methods in different scenarios of spatial confounding. Results reflect that the spatial+ method seems to provide fixed effects estimates closest to the true value although standard errors could be inflated.
View Full-Text R code available at GitHub repository
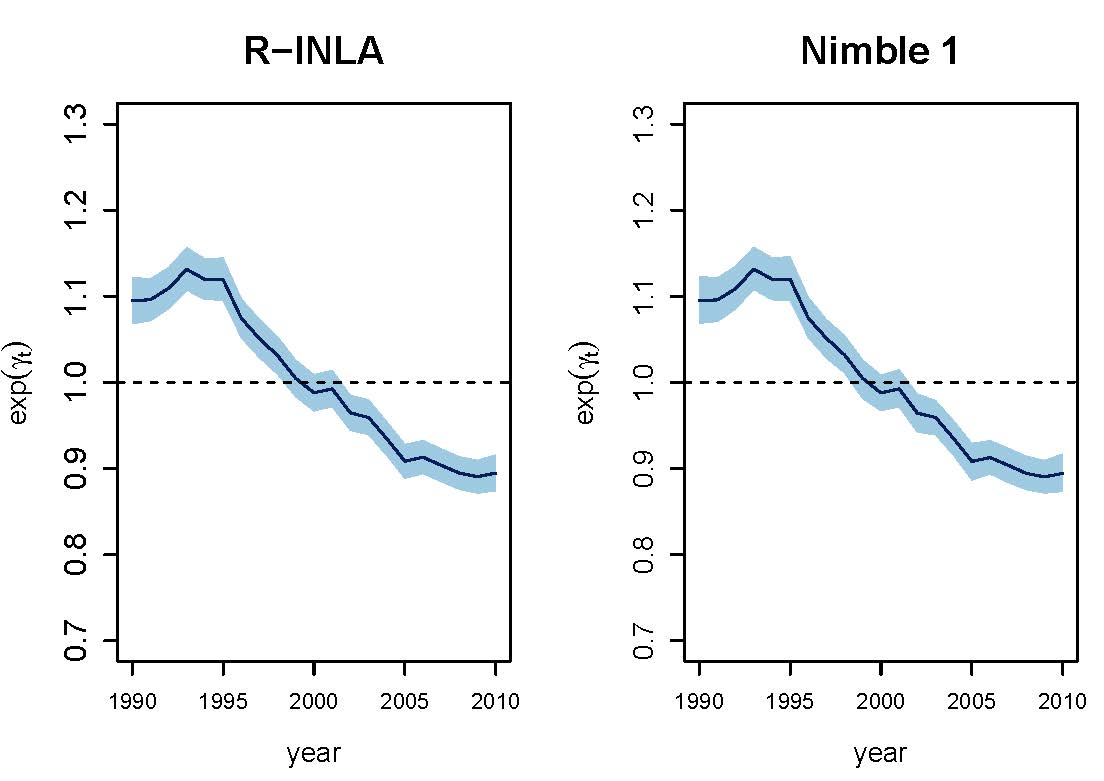
Space-time interactions in Bayesian disease mapping with recent tools: Making things easier for practitioners
Spatio-temporal disease mapping studies the distribution of mortality or incidence risks in space and its evolution in time, and it usually relies on fitting hierarchical Poisson mixed models. These models are complex for practitioners as they generally require adding constraints to correctly identify and interpret the different model terms. However, including constraints may not be straightforward in some recent software packages. This paper focuses on NIMBLE, a library of algorithms that contains among others a configurable system for Markov chain Monte Carlo (MCMC) algorithms. In particular, we show how to fit different spatio-temporal disease mapping models with NIMBLE making emphasis on how to include sum-to-zero constraints to solve identifiability issues when including spatio-temporal interactions. Breast cancer mortality data in Spain during the period 1990-2010 is used for illustration purposes. A simulation study is also conducted to compare NIMBLE with R-INLA in terms of parameter estimates and relative risk estimation. The results are very similar but differences are observed in terms of computing time.
View Full-Text R code available at GitHub repository
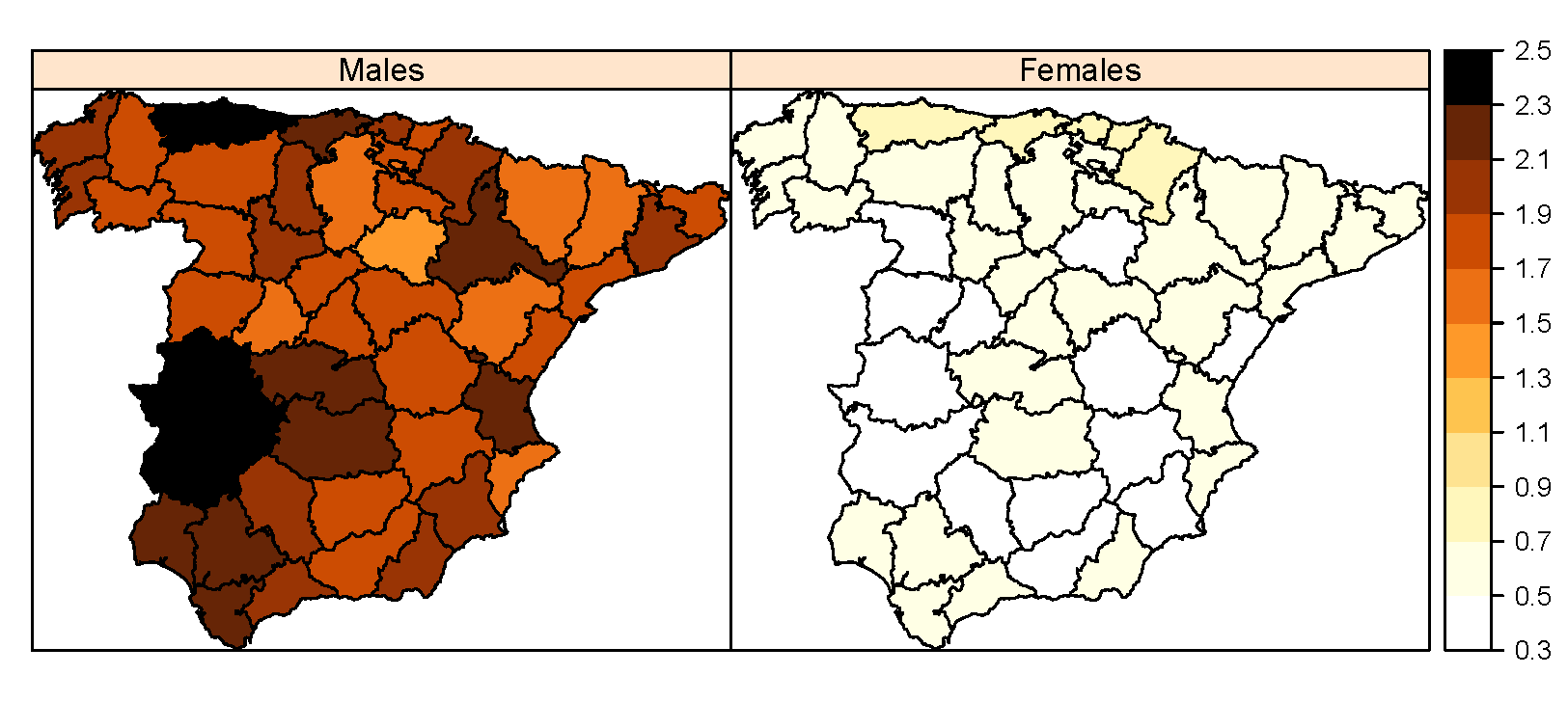
Estimating LOCP cancer mortality rates in small domains in Spain by using its relationship with lung cancer
The distribution of lip, oral cavity, and pharynx (LOCP) cancer mortality rates in small domains (defined as the combination of region, age-group, and gender) remains unknown in Spain. The scarce number of LOCP cases in each domain makes the fitting of univariate spatial models difficult. In this paper, we use the relationship of LOCP and lung cancer with tobacco consumption to define age and gender-specific shared component models. These models are useful to analyze two cancers jointly, borrowing information among them, and allowing ultimately the analysis of cancer sites with few cases at a very disaggregated level. Results show that males have higher mortality rates than females and these rates increase with age. Regions located in the north of Spain in which manufacturing industries have strong presence, as for example Burgos, show the highest LOCP mortality rates.
View Full-Text R code available at GitHub repository
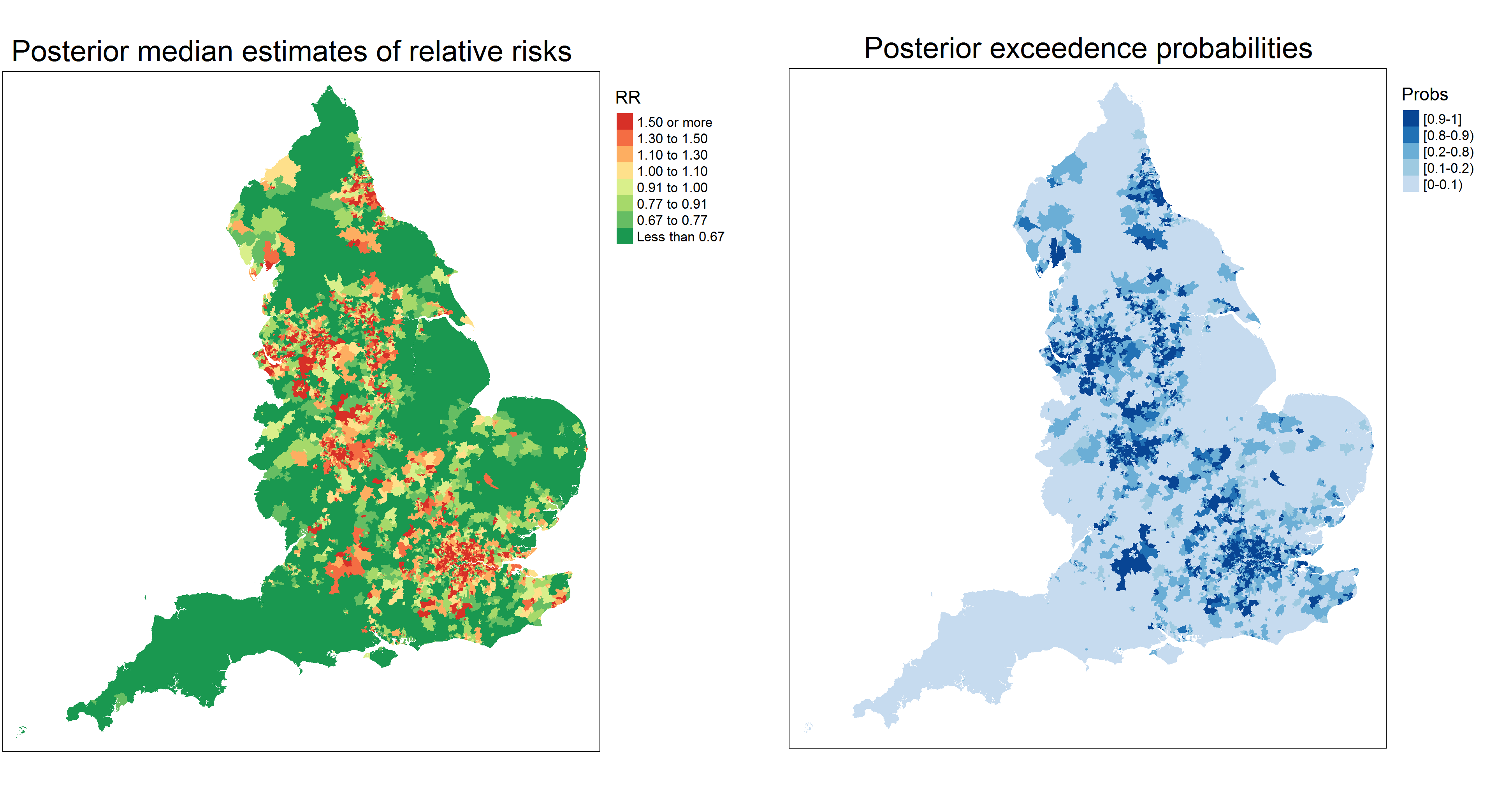
Identifying extreme COVID-19 mortality risks in English small areas: a disease cluster approach
The COVID-19 pandemic is having a huge impact worldwide and has highlighted the extent of health inequalities between countries but also in small areas within a country. Identifying areas with high mortality is important both of public health mitigation in COVID-19 outbreaks, and of longer term efforts to tackle social inequalities in health. In this paper we consider different statistical models and an extension of a recent method to analyze COVID-19 related mortality in English small areas during the first wave of the epidemic in the first half of 2020. We seek to identify hotspots, and where they are most geographically concentrated, taking account of observed area factors as well as spatial correlation and clustering in regression residuals, while also allowing for spatial discontinuities. Results show an excess of COVID-19 mortality cases in small areas surrounding London and in other small areas in North-East and and North-West of England. Models alleviating spatial confounding show ethnic isolation, air quality and area morbidity covariates having a significant and broadly similar impact on COVID-19 mortality, whereas nursing home location seems to be slightly less important.
View Full-Text R code available at GitHub repository
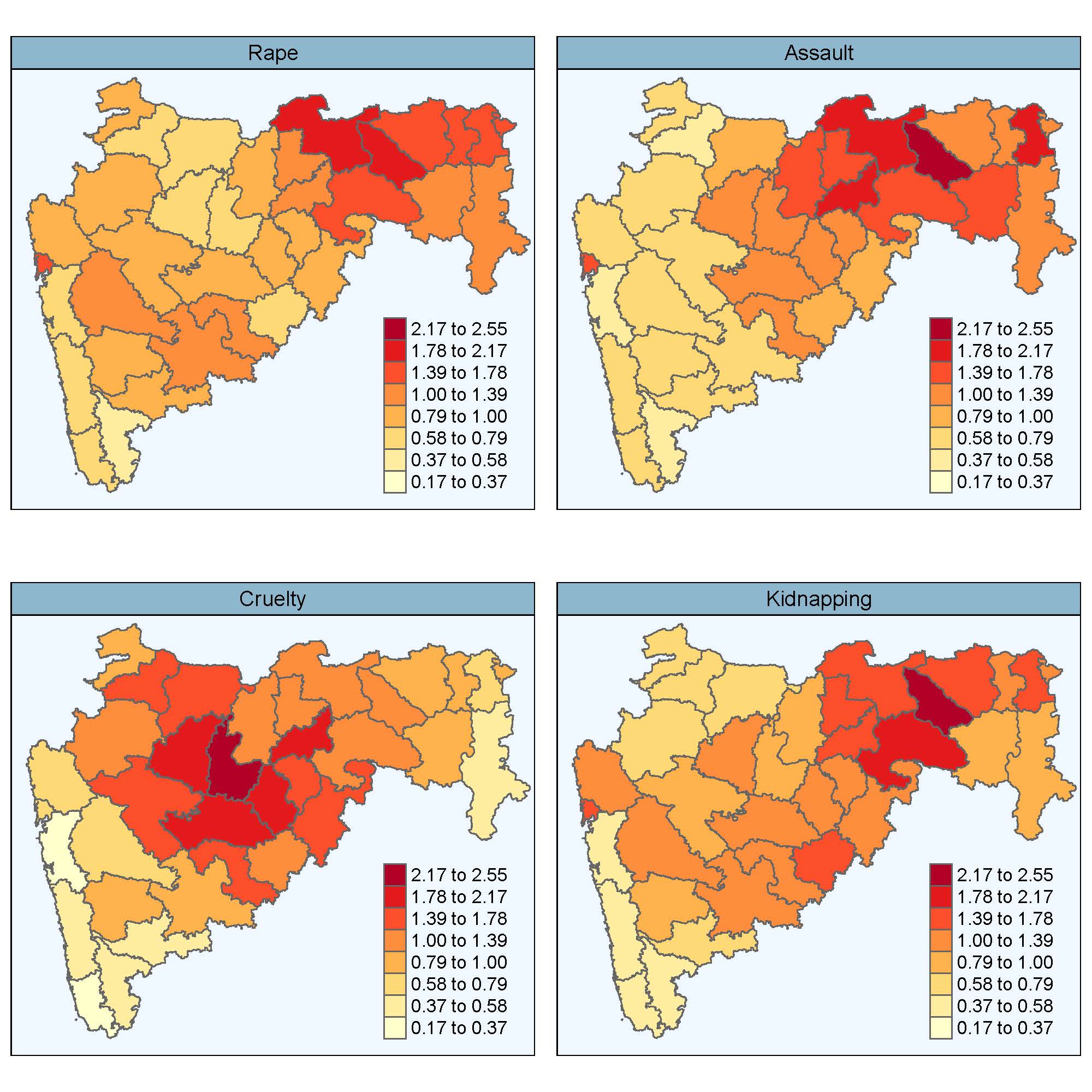
Multivariate Bayesian spatio-temporal P-spline models to analyse crimes against women
Univariate spatio-temporal models for areal count data have received great attention in recent years for estimating risks. However, models for studying multivariate responses are less commonly used mainly due to the computational burden.
In this work, multivariate spatio-temporal P-spline models are proposed to study different forms of violence against women. Modelling distinct crimes jointly improves the precision of estimates over univariate models and allows to compute correlations among them. The correlation between the spatial and the temporal patterns may suggest connections among the different crimes that will certainly benefit a thorough comprehension of this problem that affects millions of women around the world.
The models are fitted using integrated nested Laplace approximations (INLA), and are used to analyse four distinct crimes against women at district level in the Indian state of Maharashtra during the period 2001-2013.
R code available at GitHub repository
Alleviating confounding in spatio-temporal areal models with an application on crimes against women in India
Assessing associations between a response of interest and a set of covariates in spatial areal models is the leitmotiv of ecological regression. However, the presence of spatially correlated random effects can mask or even bias estimates of such associations due to confounding effects if they are not carefully handled. Though potentially harmful, confounding issues have often been ignored in practice leading to wrong conclusions about the underlying associations between the response and the covariates. In spatio-temporal areal models, the temporal dimension may emerge as a new source of confounding, and the problem may be even worse. In this work, we propose two approaches to deal with confounding of fixed effects by spatial and temporal random effects, while obtaining good model predictions. In particular, restricted regression and an apparently -though in fact not- equivalent procedure using constraints are proposed within both fully Bayes and empirical Bayes approaches. The methods are compared in terms of fixed-effect estimates and model selection criteria. The techniques are used to assess the association between dowry deaths and certain socio-demographic covariates in the districts of Uttar Pradesh, India.
View Full-Text R code available at GitHub repository
Scalable Bayesian modelling for smoothing disease risks in large spatial data sets using INLA
Several methods have been proposed in the spatial statistics literature to analyse big data sets in continuous domains. However, new methods for analysing high-dimensional areal data are still scarce. Here, we propose a scalable Bayesian modelling approach for smoothing mortality (or incidence) risks in highdimensional data, that is, when the number of small areas is very large. The method is implemented in the R add-on package bigDM and it is based on the idea of "divide and conquer". Although this proposal could possibly be implemented using any Bayesian fitting technique, we use INLA here (integrated nested Laplace approximations) as it is now a well-known technique, computationally efficient, and easy for practitioners to handle. We analyse the proposal’s empirical performance in a comprehensive simulation study that considers two model-free settings. Finally, the methodology is applied to analyse male colorectal cancer mortality in Spanish municipalities showing its benefits with regard to the standard approach in terms of goodness of fit and computational time.
View Full-Text R package bigDM available at GitHub repository
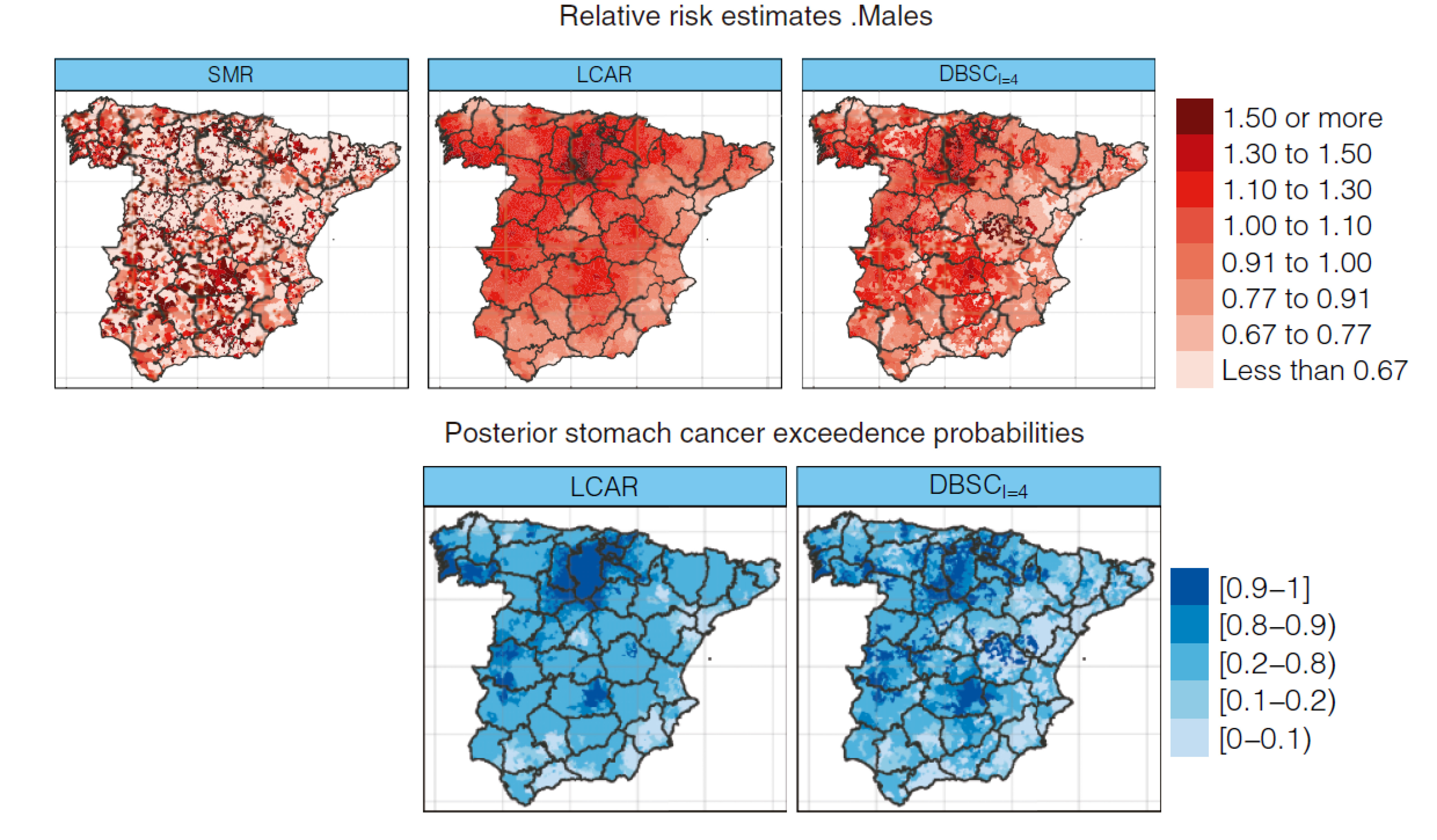
Dealing with risk discontinuities to estimate cancer mortality risks when the number of small areas is large
Many statistical models have been developed during the last years to smooth risks in disease mapping. However, most of these modeling approaches do not take possible local discontinuities into consideration or if they do, they are computationally prohibitive or simply do not work when the number of small areas is large. In this paper, we propose a two-step method to deal with discontinuities and to smooth noisy risks in small areas. In a first stage, a novel density-based clustering algorithm is used. In contrast to previous proposals, this algorithm is able to automatically detect the number of spatial clusters, thus providing a single cluster structure. In the second stage, a Bayesian hierarchical spatial model that takes the cluster configuration into account is fitted, which accounts for the discontinuities in disease risk. To evaluate the performance of this new procedure in comparison to previous proposals, a simulation study has been conducted. Results show competitive risk estimates at a much better computational cost. The new methodology is used to analyze stomach cancer mortality data in Spanish municipalities.
View Full-Text R code available at GitHub repository
Bayesian inference in multivariate spatio-temporal areal models using INLA: analysis of gender-based violence in small areas
Multivariate models for spatial count data are currently receiving attention in disease mapping to model two or more diseases jointly. They have been thoroughly studied from a theoretical point of view, but their use in practice is still limited because they are computationally expensive and, in general, they are not implemented in standard software to be used routinely. Here, a new multivariate proposal, based on the recently derived M models for spatial data, is developed for spatio-temporal areal data. The model takes account of the correlation between the spatial and temporal patterns of the phenomena being studied, and it also includes spatio-temporal interactions. Though multivariate models have been traditionally fitted using Markov chain Monte Carlo techniques, here we propose to adopt integrated nested Laplace approximations to speed up computations as results obtained using both fitting techniques were nearly identical. The techniques are used to analyse two forms of crimes against women in India. In particular, we focus on the joint analysis of rapes and dowry deaths in Uttar Pradesh, the most populated Indian state, during the years 2001–2014.
View Full-Text R code available at GitHub repository
Space-time analysis of ovarian cancer mortality rates by age group in Spanish provinces (1989-2015)
Ovarian cancer is a silent and largely asymptomatic cancer, leading to late diagnosis and worse prognosis. The late-stage detection and low survival rates, makes the study of the space-time evolution of ovarian cancer particularly relevant. In addition, research of this cancer in small areas (like provinces or counties) is still scarce. The study presented here covers all ovarian cancer deaths for women over 50 years of age in the provinces of Spain during the period 1989-2015. Spatio-temporal models have been fitted to smooth ovarian cancer mortality rates in age groups [50,60), [60,70), [70,80), and [80,+), borrowing information from spatial and temporal neighbours. Model fitting and inference has been carried out using the Integrated Nested Laplace Approximation (INLA) technique. Large differences in ovarian cancer mortality among the age groups have been found, with higher mortality rates in the older age groups. Striking differences are observed between northern and southern Spain. The global temporal trends (by age group) reveal that the evolution of ovarian cancer over the whole of Spain has remained nearly constant since the early 2000s. Differences in ovarian cancer mortality exist among the Spanish provinces, years, and age groups. As the exact causes of ovarian cancer remain unknown, spatio-temporal analyses by age groups are essential to discover inequalities in ovarian cancer mortality. Women over 60 years of age should be the focus of follow-up studies as the mortality rates remain constant since 2002. High-mortality provinces should also be monitored to look for specific risk factors.
View Full-Text

Crime against women in India: unveiling spatial patterns and temporal trends of dowry deaths in the districts of Uttar Pradesh
Crimes against women in India have been continuously increasing lately as reported by the National Crime Records Bureau. Gender-based violence has become a serious issue to such an extent that it has been catalogued as a high-impact health problem by the World Health Organization. However, there is a lack of spatio-temporal analyses to reveal a complete picture of the geographical and temporal patterns of crimes against women. In this paper, we focus on analysing how the geographical pattern of dowry deaths changes over time in the districts of Uttar Pradesh during the period 2001-2014. The study of the geographical distribution of dowry death incidence and its evolution over time aims to identify specific regions that exhibit high risks and hypothesize on potential risk factors. We also look into different spatial priors and their effects on final risk estimates. Various priors for the hyperparameters are also reviewed. Risk estimates seem to be robust in terms of the spatial prior and hyperprior choices and final results highlight several districts with extreme risks of dowry death incidence. Statistically significant associations are also found between dowry deaths, sex ratio, and some forms of overall crime.
View Full-Text R code available at GitHub repository
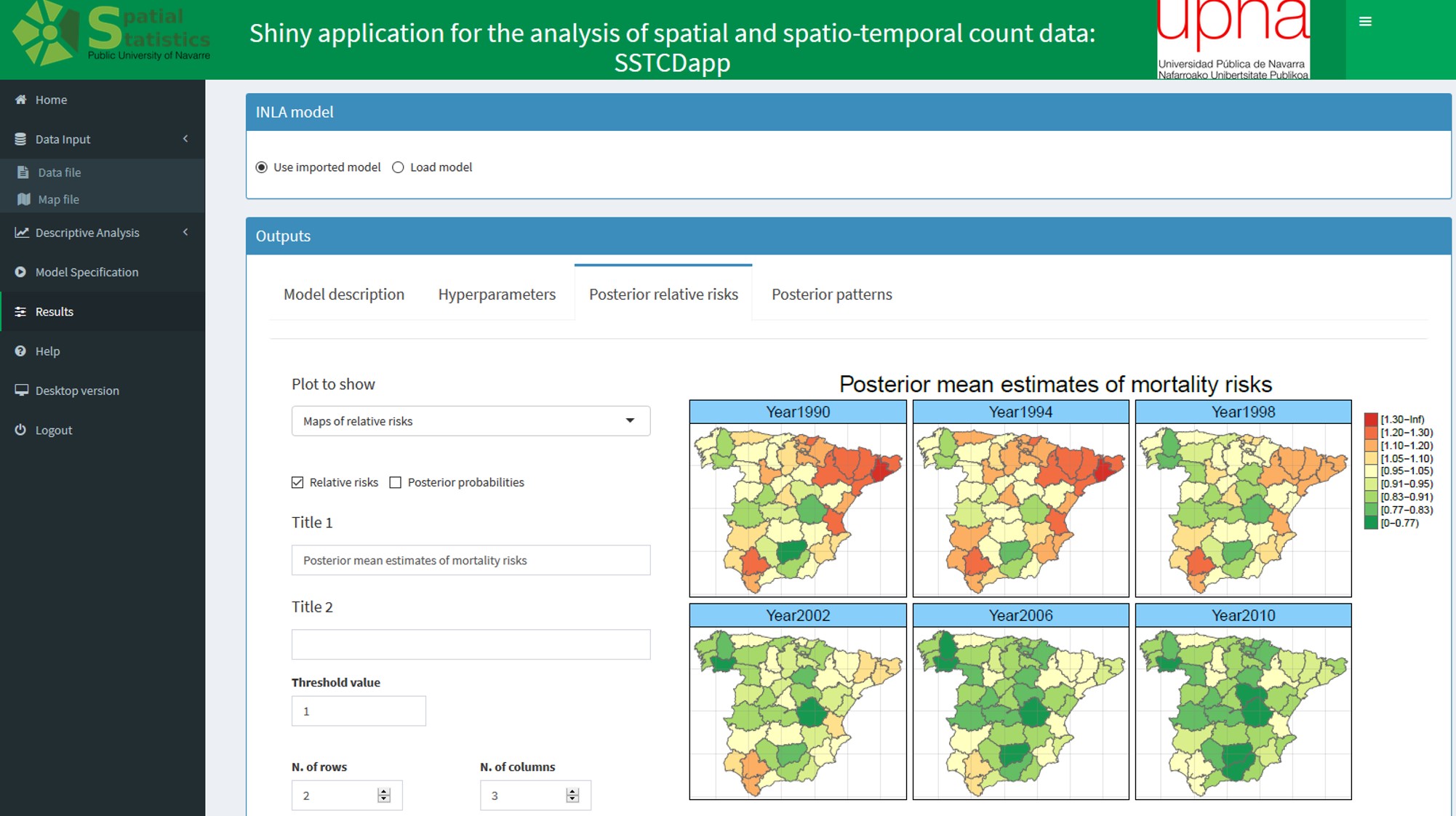
SSTCDapp WEB APPLICATION
An interactive and user-friendly web application designed to fit an extensive range of fairly complex spatio-temporal models to smooth the very often extremely variable standardized incidence/mortality risks or crude rates. The application is built with the R package shiny and relies on the well-founded integrated nested Laplace approximation technique for model fitting and inference. Although SSTCDapp is simple to use, the underlying statistical theory is well founded and all key issues such as model identifiability, model selection, and several spatial priors and hyperpriors for sensitivity analyses are properly addressed.
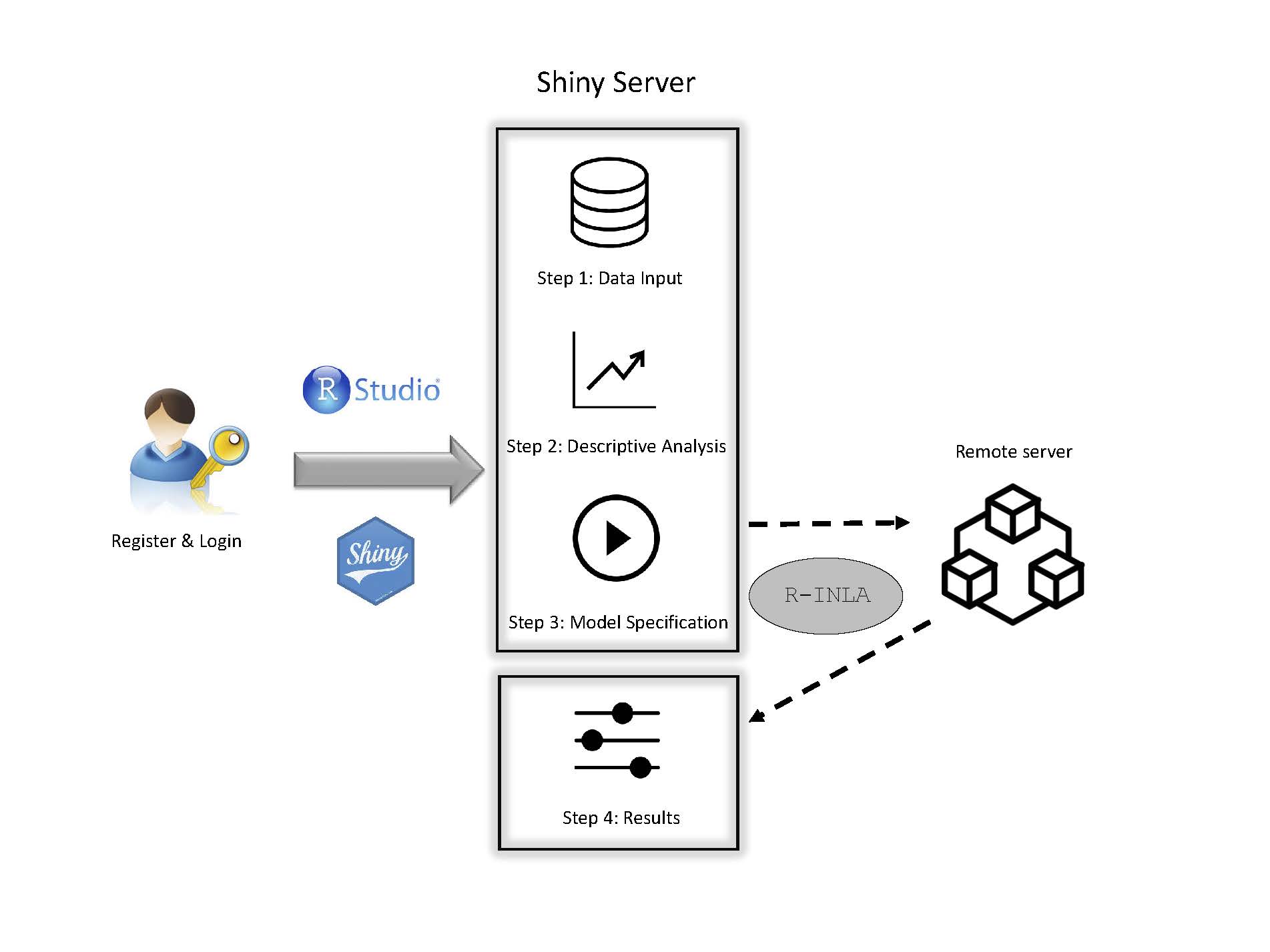
Online relative risks/rates estimation in spatial and spatio-temporal disease mapping
Spatial and spatio-temporal analyses of count data are crucial in epidemiology and other fields to unveil spatial and spatio-temporal patterns of incidence and/or mortality risks. However, fitting spatial and spatio-temporal models is not easy for non-expert users. The objective of this paper is to present an interactive and user-friendly web application (named SSTCDapp) for the analysis of spatial and spatio-temporal mortality or incidence data. Although SSTCDapp is simple to use, the underlying statistical theory is well founded and all key issues such as model identifiability, model selection, and several spatial priors and hyperpriors for sensitivity analyses are properly addressed. The web application is designed to fit an extensive range of fairly complex spatio-temporal models to smooth the very often extremely variable standardized incidence/mortality risks or crude rates. The application is built with the R package shiny and relies on the well founded integrated nested Laplace approximation technique for model fitting and inference. The use of the web application is shown through the analysis of Spanish spatio-temporal breast cancer data. Different possibilities for the analysis regarding the type of model, model selection criteria, and a range of graphical as well as numerical outputs are provided. Unlike other software used in disease mapping, SSTCDapp facilitates the fit of complex statistical models to non-experts users without the need of installing any software in their own computers, since all the analyses and computations are made in a powerful remote server. In addition, a desktop version is also available to run the application locally in those cases in which data confidentiality is a serious issue.
View Full-Text
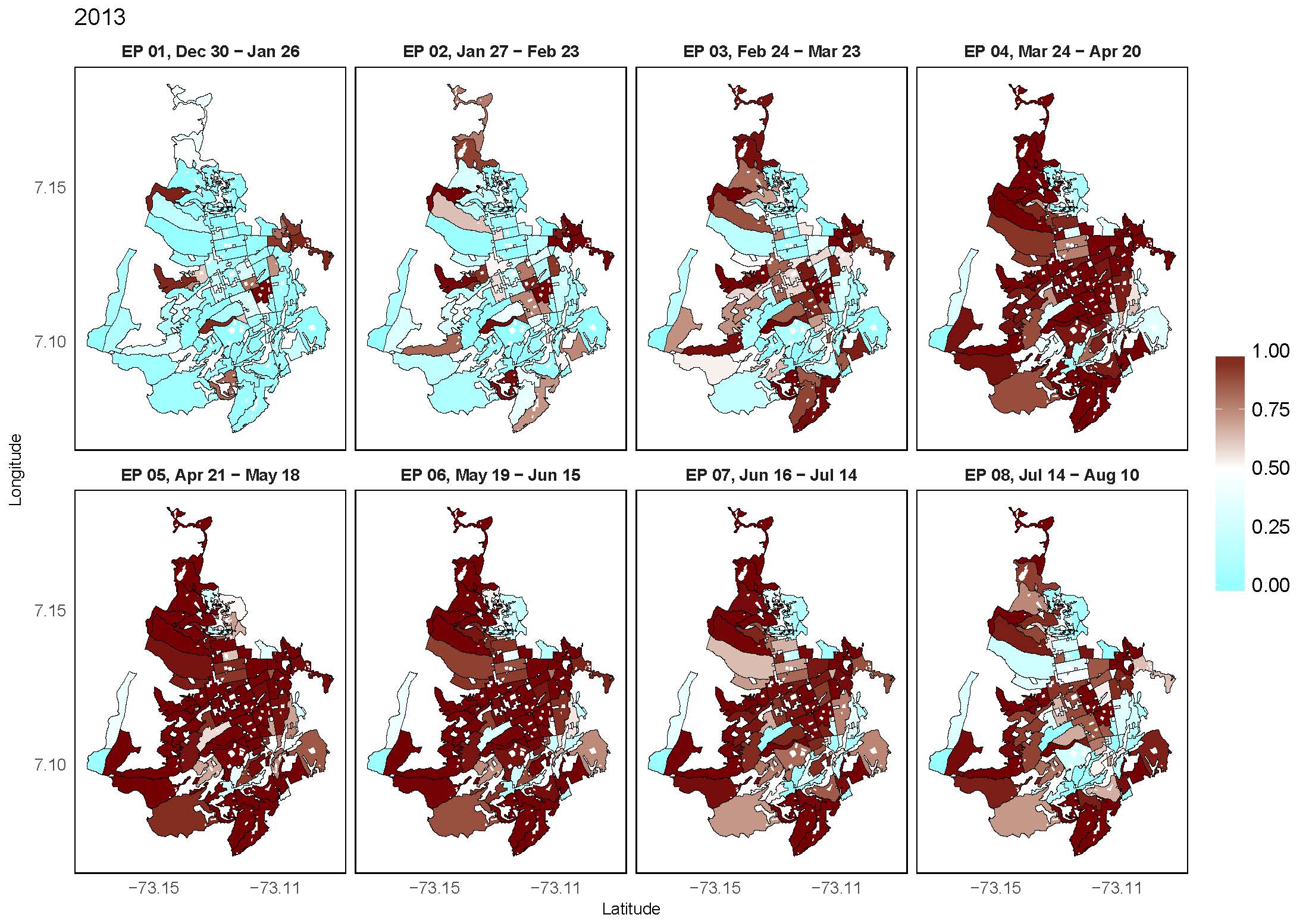
Two-level resolution of relative risk of dengue disease in a hyperendemic city of Colombia
Risk maps of dengue disease offer to the public health officers a tool to model disease risk in space and time. We analyzed the geographical distribution of relative incidence risk of dengue disease in a high incidence city from Colombia, and its evolution in time during the period January 2009—December 2015, identifying regional effects at different levels of spatial aggregations. Cases of dengue disease were geocoded and spatially allocated to census sectors, and temporally aggregated by epidemiological periods. The census sectors are nested in administrative divisions defined as communes, configuring two levels of spatial aggregation for the dengue cases. Spatio-temporal models including census sector and commune-level spatially structured random effects were fitted to estimate dengue incidence relative risks using the integrated nested Laplace approximation (INLA) technique. The final selected model included two-level spatial random effects, a global structured temporal random effect, and a census sector-level interaction term. Risk maps by epidemiological period and risk profiles by census sector were generated from the modeling process, showing the transmission dynamics of the disease. All the census sectors in the city displayed high risk at some epidemiological period in the outbreak periods. Relative risk estimation of dengue disease using INLA offered a quick and powerful method for parameter estimation and inference.
View Full-Text
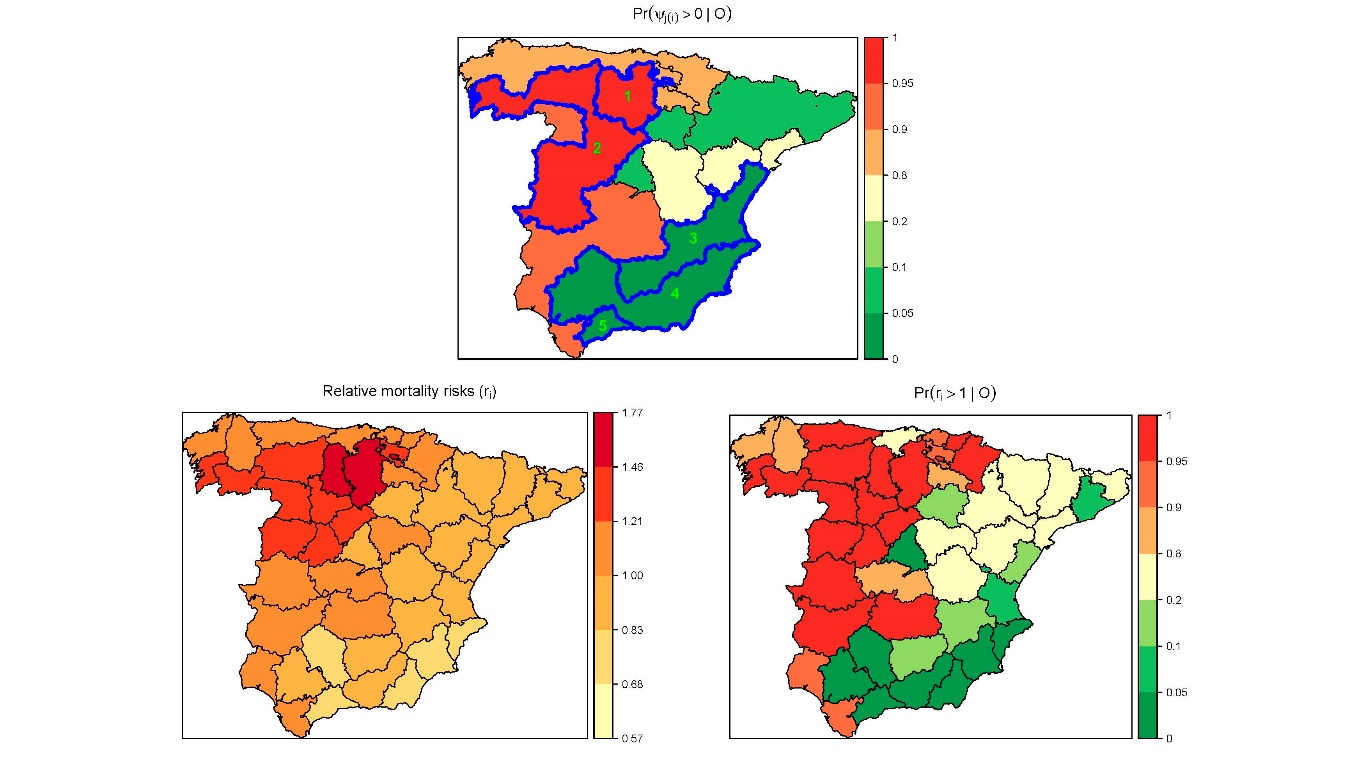
A two-stage approach to estimate spatial and spatio-temporal disease risks in the presence of local discontinuities and clusters
Disease risk maps for areal unit data are often estimated from Poisson mixed models with local spatial smoothing, for example by incorporating random effects with a conditional autoregressive prior distribution. However, one of the limitations is that local discontinuities in the spatial pattern are not usually modelled, leading to over-smoothing of the risk maps and a masking of clusters of hot/coldspot areas. In this paper, we propose a novel two-stage approach to estimate and map disease risk in the presence of such local discontinuities and clusters. We propose approaches in both spatial and spatio-temporal domains, where for the latter the clusters can either be fixed or allowed to vary over time. In the first stage, we apply an agglomerative hierarchical clustering algorithm to training data to provide sets of potential clusters, and in the second stage, a two-level spatial or spatio-temporal model is applied to each potential cluster configuration. The superiority of the proposed approach with regard to a previous proposal is shown by simulation, and the methodology is applied to two important public health problems in Spain, namely stomach cancer mortality across Spain and brain cancer incidence in the Navarre and Basque Country regions of Spain.
View Full-Text R code available at GitHub repository
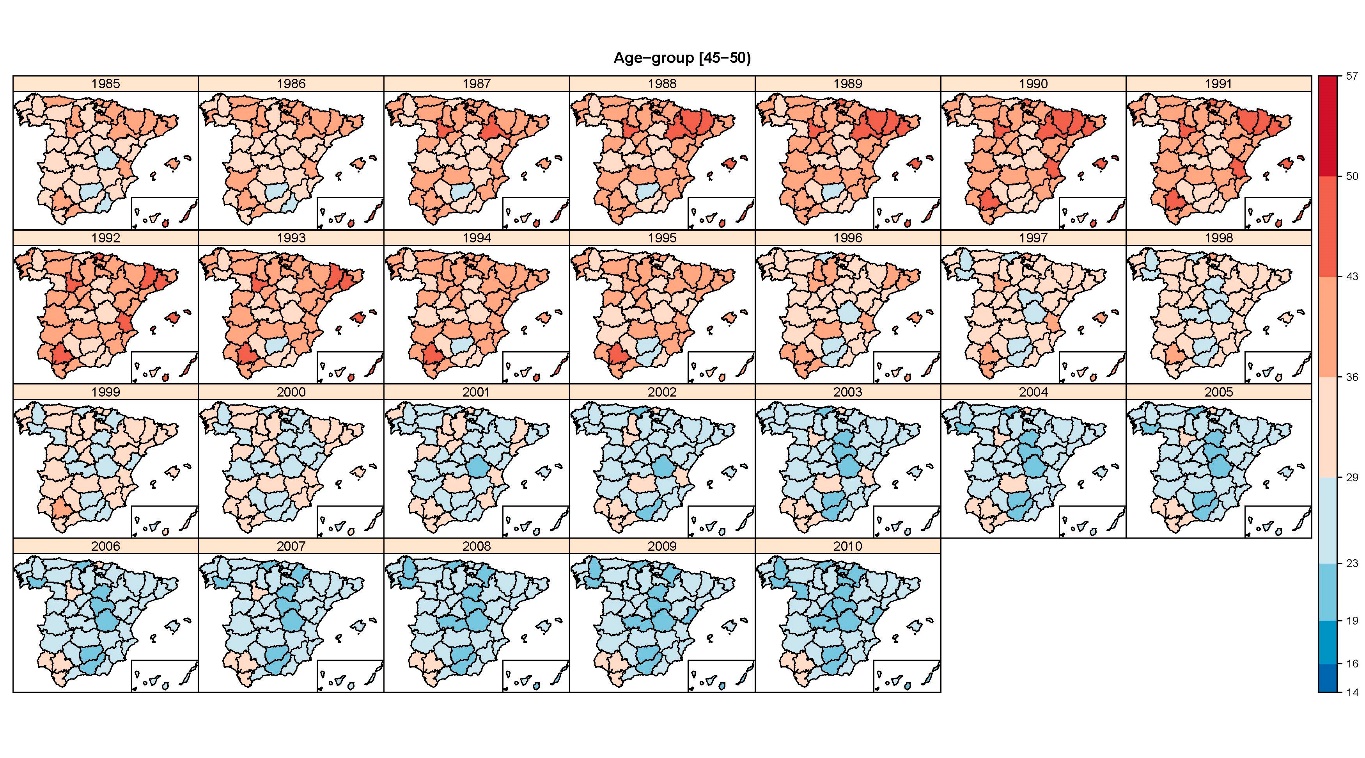
Flexible Bayesian P-splines for smoothing age-specific spatio-temporal mortality patterns
In this paper age–space–time models based on one and two-dimensional P-splines with B-spline bases are proposed for smoothing mortality rates, where both fixed relative scale and scale invariant two-dimensional penalties are examined. Model fitting and inference are carried out using integrated nested Laplace approximations, a recent Bayesian technique that speeds up computations compared to McMC methods. The models will be illustrated with Spanish breast cancer mortality data during the period 1985–2010, where a general decline in breast cancer mortality has been observed in Spanish provinces in the last decades. The results reveal that mortality rates for the oldest age groups do not decrease in all provinces.
View Full-Text R code available at GitHub repository
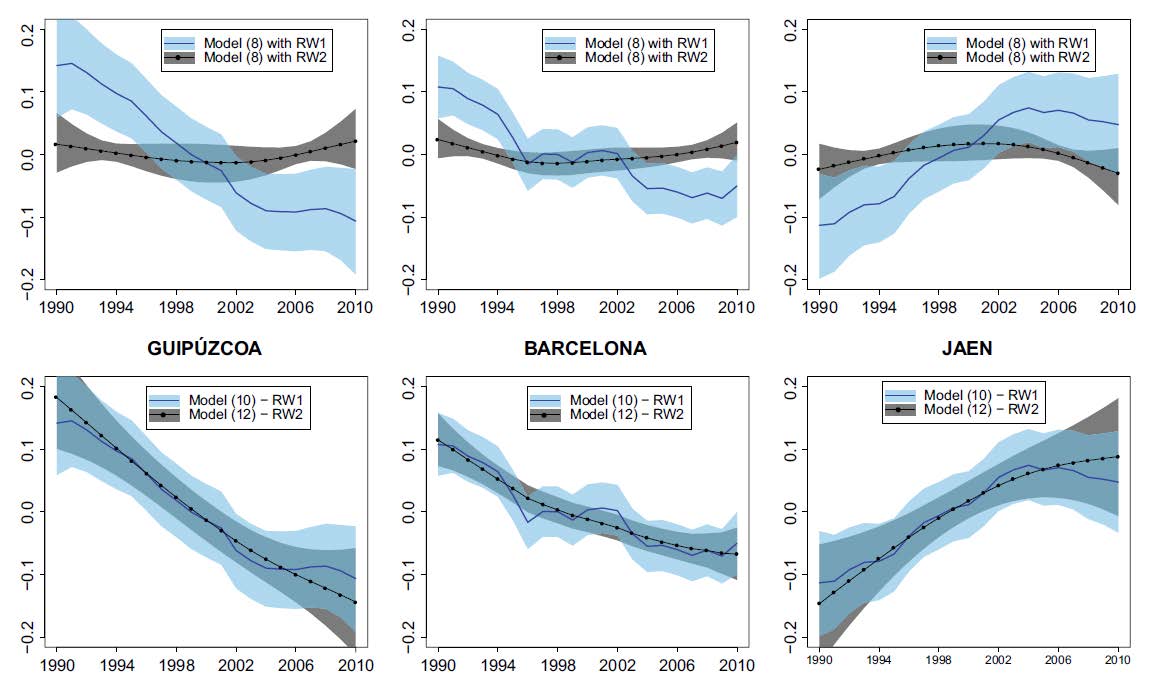
In spatio-temporal disease mapping models, identifiability constraints affect PQL and INLA results
Disease mapping studies the distribution of relative risks or rates in space and time, and typically relies on generalized linear mixed models (GLMMs) including fixed effects and spatial, temporal, and spatio-temporal random effects. These GLMMs are typically not identifiable and constraints are required to achieve sensible results. However, automatic specification of constraints can sometimes lead to misleading results. In particular, the penalized quasi-likelihood fitting technique automatically centers the random effects even when this is not necessary. In the Bayesian approach, the recently-introduced integrated nested Laplace approximations computing technique can also produce wrong results if constraints are not well-specified. In this paper the spatial, temporal, and spatio-temporal interaction random effects are reparameterized using the spectral decompositions of their precision matrices to establish the appropriate identifiability constraints. Breast cancer mortality data from Spain is used to illustrate the ideas.
View Full-Text R code available at GitHub repository
One-dimensional, two-dimensional, and three-dimensional B-splines to specify space-time interactions in Bayesian disease mapping: model fitting and model identifiability
In recent years, models incorporating splines have been considered for smoothing risks in disease mapping. Although these models are very flexible, they can be computationally demanding in certain cases. In this work, one, two, and three-dimensional B-splines (penalized or unpenalized) are considered to model space–time interactions. Model identifiability issues are discussed and appropriate constraints are clearly established. As computing time could be a limitation in real practice, integrated nested Laplace approximations are used for model fitting and inference. The complete set of proposed models are illustrated using cancer mortality data in small areas. We conclude that if the number of small areas is not big, one dimensional P-splines for the space–time interaction could be a good choice. When the number of small areas increases substantially, two-dimensional and mainly three dimensional splines are computationally better alternatives.
View Full-Text
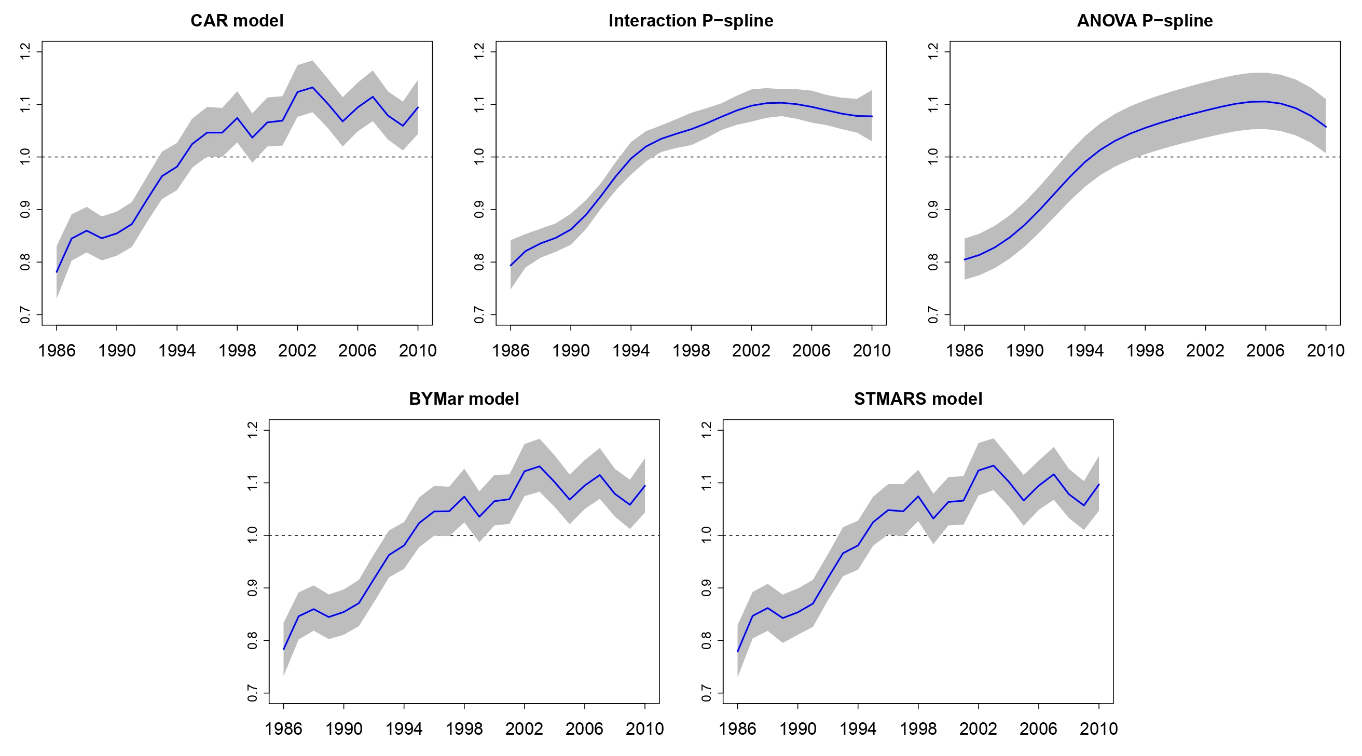
Smoothing and high risk areas detection in space-time disease mapping: a comparison of P-splines, autoregressive, and moving average models
Recently, several models have been proposed for smoothing risks in disease mapping. These models consider different ways of introducing both spatial and temporal dependence as well as spatio-temporal interactions. In this work, a comparison among some autoregressive, moving average, and P-spline models is performed. Firstly, brain cancer mortality data are used to analyze the degree of smoothness introduced by these models. Secondly, two separate simulation studies (one model-based and the other model-free) are carried out to evaluate the model performance in terms of bias, variability, sensitivity, and specificity. We conclude that P-spline models seem to be a good alternative to autoregressive and moving average models when analyzing highly sparse disease mapping data
View Full-Text
Two-level spatially structured models in spatio-temporal disease mapping
This work focuses on extending some classical spatio-temporal models in disease mapping. The objective is to present a family of flexible models to analyze real data naturally organized in two different levels of spatial aggregation like municipalities within health areas or provinces, or counties within states. Model fitting and inference will be carried out using integrated nested Laplace approximations. The performance of the new models compared to models including a single spatial random effect is assessed by simulation. Results show good behavior of the proposed two-level spatially structured models in terms of several criteria. Brain cancer mortality data in the municipalities of two regions in Spain will be analyzed using the new model proposals. It will be shown that a model with two-level spatial random effects overcomes the usual single-level models.
View Full-Text
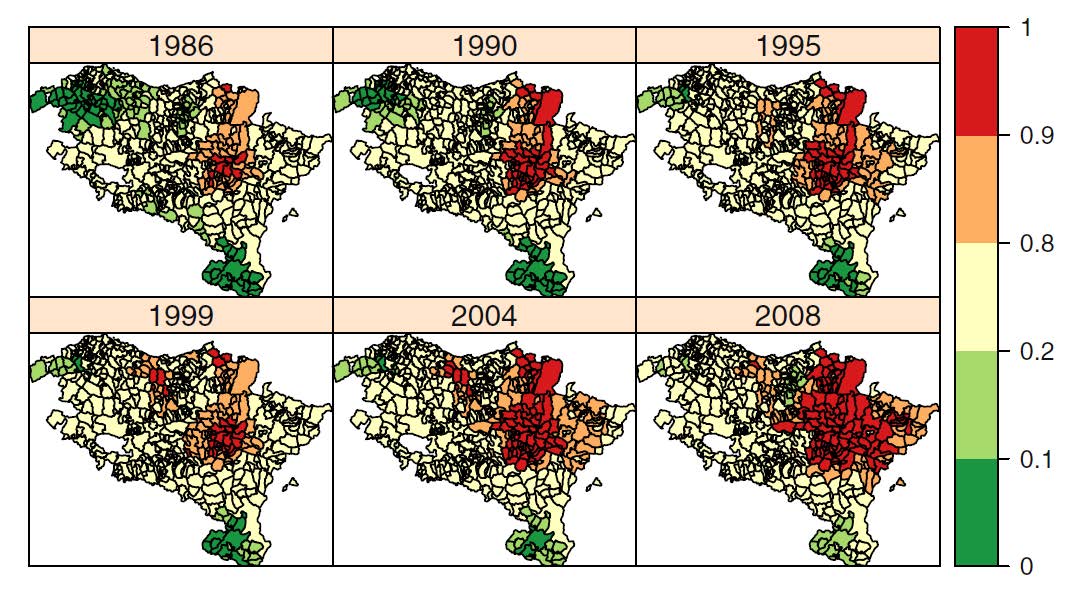
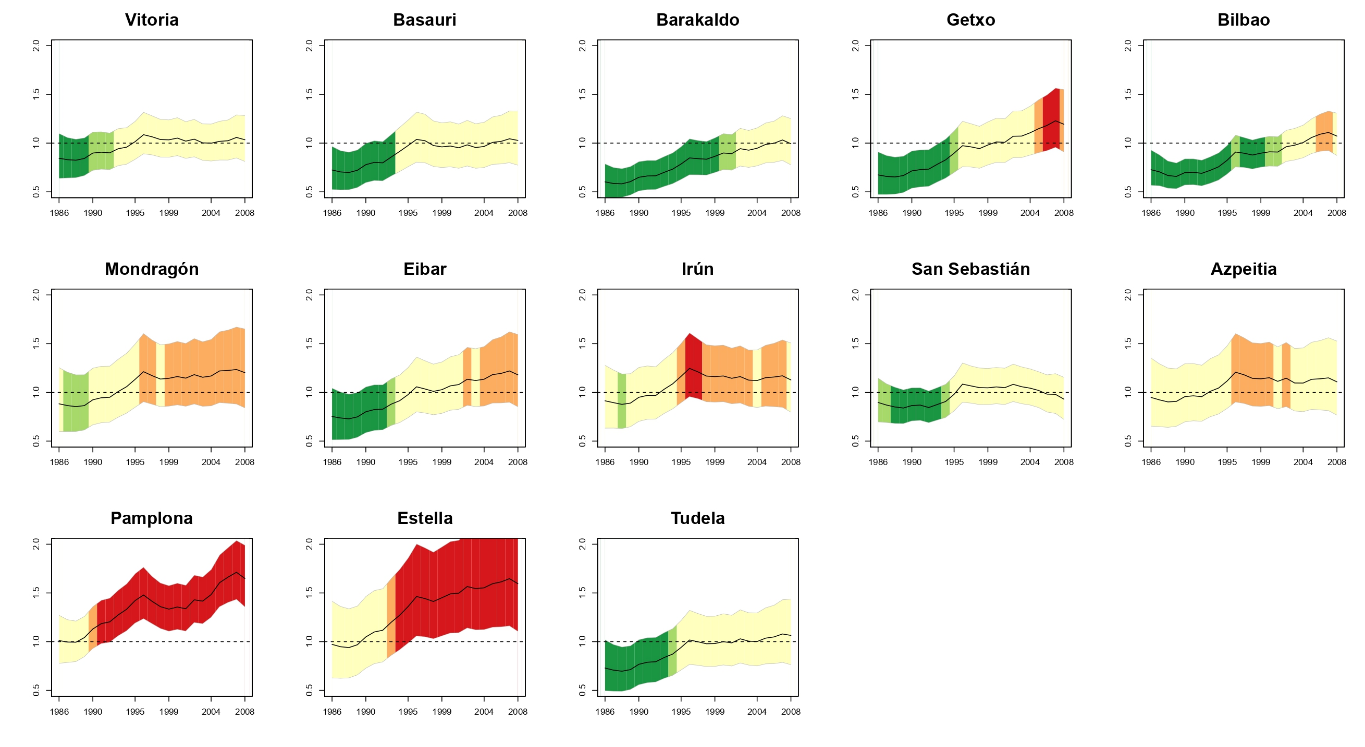
Temporal evolution of brain cancer incidence in the municipalities of Navarre and the Basque Country, Spain
Brain cancer incidence rates in Spain are below the European’s average. However, there are two regions in the north of the country, Navarre and the Basque Country, ranked among the European regions with the highest incidence rates for both males and females. Our objective here was two-fold. Firstly, to describe the temporal evolution of the geographical pattern of brain cancer incidence in Navarre and the Basque Country, and secondly, to look for specific high risk areas (municipalities) within these two regions in the study period (1986–2008). A mixed Poisson model with two levels of spatial effects is used. The model also included two levels of spatial effects (municipalities and local health areas). Model fitting was carried out using penalized quasi-likelihood. High risk regions were detected using upper one-sided confidence intervals. Results revealed a group of high risk areas surrounding Pamplona, the capital city of Navarre, and a few municipalities with significant high risks in the northern part of the region, specifically in the border between Navarre and the Basque Country (Gipuzkoa). The global temporal trend was found to be increasing. Differences were also observed among specific risk evolutions in certain municipalities.
View Full-Text
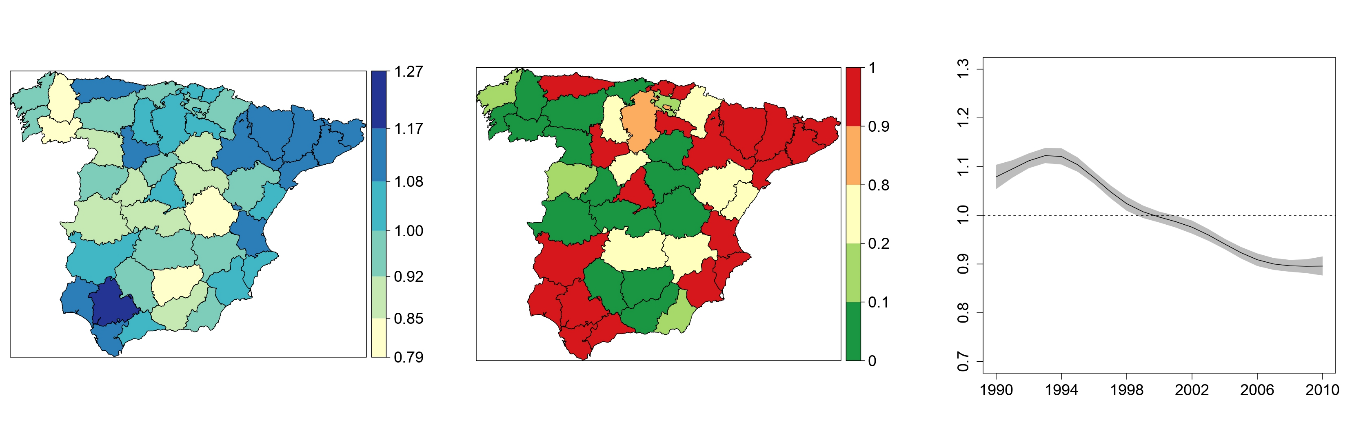
Analyzing the evolution of young people brain cancer mortality in Spanish provinces
In this paper, our objective is to analyze the spatio-temporal evolution of brain cancer relative mortality risks in young population (under 20 years of age) in Spanish provinces during the period 1986–2010. For this purpose, a new and flexible conditional autoregressive spatio-temporal model with two levels of spatial aggregation was used. We observe that brain cancer relative mortality risks in young population in Spanish provinces decreased during the last years, although a clear increase was observed during the 1990s. The global geographical pattern emphasized a high relative mortality risk in Navarre and a low relative mortality risk in Madrid. Although there is a specific Autonomous Region–time interaction effect on the relative mortality risks this effect is weak in the final estimates when compared to the global spatial and temporal effects.
View Full-Text
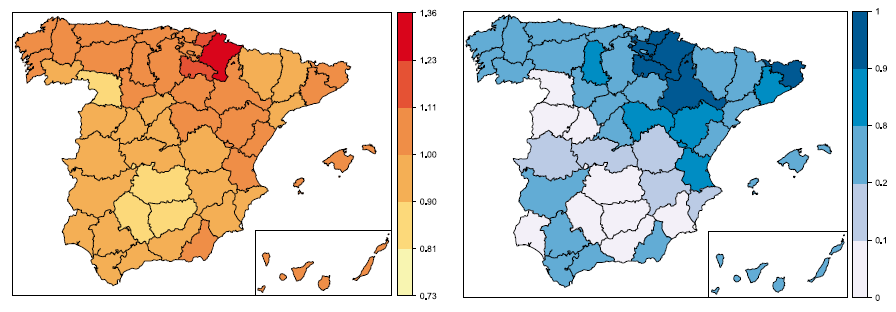
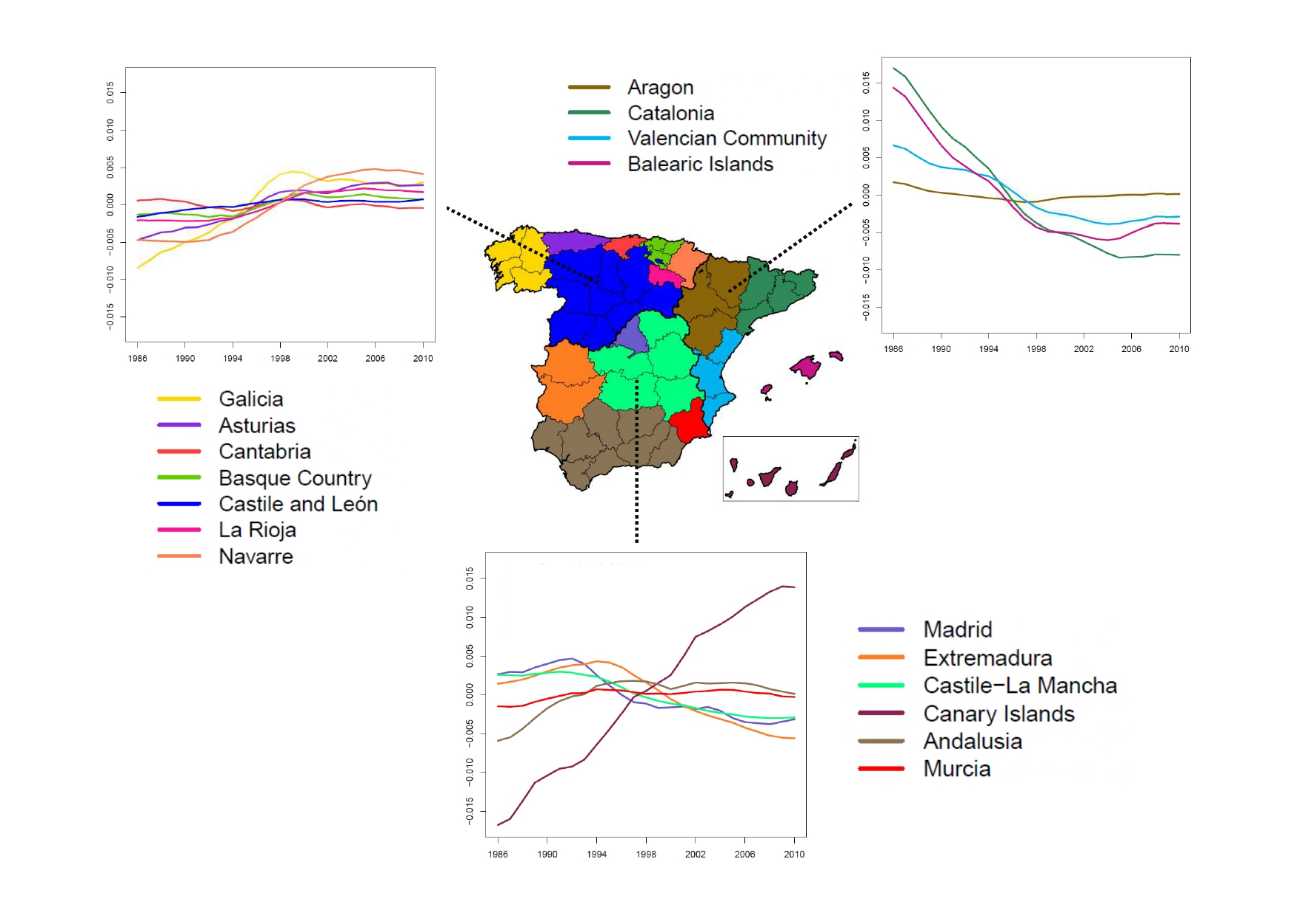
On fitting spatio-temporal disease mapping models using approximate Bayesian inference
Spatio-temporal disease mapping comprises a wide range of models used to describe the distribution of a disease in space and its evolution in time. These models have been commonly formulated within a hierarchical Bayesian framework with two main approaches: an empirical Bayes (EB) and a fully Bayes (FB) approach. The EB approach provides point estimates of the parameters relying on the well-known penalized quasi-likelihood (PQL) technique. The FB approach provides the posterior distribution of the target parameters. These marginal distributions are not usually available in closed form and common estimation procedures are based on Markov chain Monte Carlo (MCMC) methods. However, the spatio-temporal models used in disease mapping are often very complex and MCMC methods may lead to large Monte Carlo errors and a huge computation time if the dimension of the data at hand is large. To circumvent these potential inconveniences, a new technique called integrated nested Laplace approximations (INLA), based on nested Laplace approximations, has been proposed for Bayesian inference in latent Gaussian models. In this paper, we show how to fit different spatio-temporal models for disease mapping with INLA using the Leroux CAR prior for the spatial component, and we compare it with PQL via a simulation study. The spatio-temporal distribution of male brain cancer mortality in Spain during the period 1986–2010 is also analysed.
View Full-Text